MEAM.Design : MEAM410-09C-L5-dynamics

MEAM.Design - MEAM 410 - L5: Balancing Act - Dynamics

(Note - we're trying embedded LaTeX typesetting on this page. You may need to download the jsMath fonts from here to properly view the equations.)

Representing our system as a wheel and body:

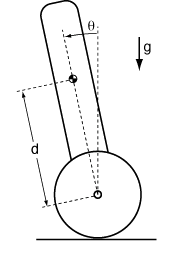
We can separate this into two free bodies:

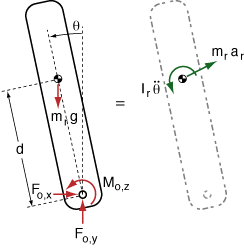
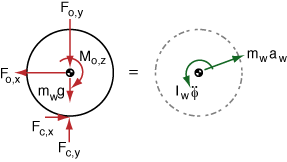
For the robot, we can sum moments about the pin (O):

{$$ (m_r g)(d \sin\theta) \hat{k} + M_{o} \hat{k} = I_r \ddot\theta \hat{k} - (-d \sin\theta \hat{i} + d \cos\theta \hat{j}) \times (m_r a_r) $$}

{$$ F_{o,x} = m_r a_r \cos\theta $$}

{$$ F_{o,y} - m_r g = m_r a_r \sin\theta $$}

And the same for the wheel, of radius {$R$}, where we can assume no slip, and that therefore {$a_w = - R\ddot{\phi}$} is horizontal:

{$$ F_{c,x} R - M_{o} = I_w \ddot\phi $$}

{$$ F_{c,x} - F_{o,x} = - m_w R \ddot{\phi} $$}

{$$ F_{c,y} - F_{o,y} - m_w g = 0 $$}