MEAM.Design - MEAM 248 - WALK - Dynamics

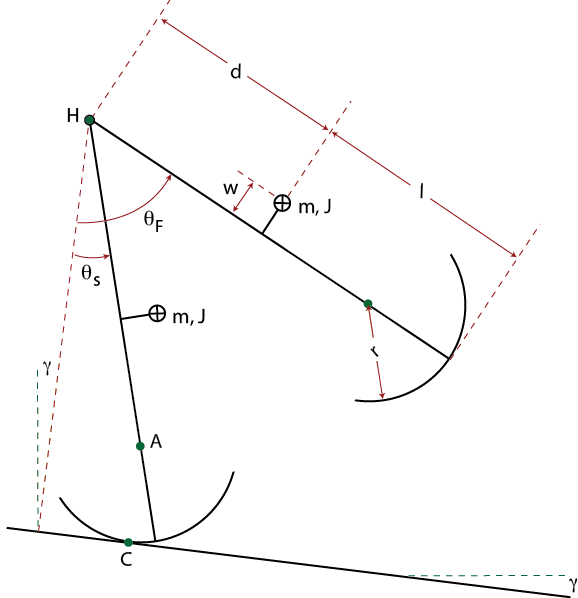
The System

We will define a straight-legged, round-footed walker using the variables and constants shown to the right. We will call the leg in contact with the ground the stance (S) leg, while the one in motion we will call the "'free"' (F) leg. Points of interest include:

($H$) - the hip
($A$) - the center of the foot arc
($C$) - the contact point with the slope
($GS$) - the CG of the stance leg
($GF$) - the CG of the free leg

Both legs are assumed to be identical, with the following constants:

($d$) - hip to CG distance
($w$) - CG offset distance
($l$) - CG to foot distance
($r$) - foot radius
($m$) - leg mass
($J$) - leg moment of inertia

And the motion will involve the following variables:

($\gamma$) - the slope angle
($\theta_S$) - the angle of the stance leg relative to the slope normal
($\theta_F$) - the angle of the free leg relative to the slope normal

We will place our coordinate frame with the X axis aligned down the slope and Y aligned with the positive surface normal.


Free-Body and Inertial-Response Diagrams

Before we can do anything useful, we need to produce a free-body and inertial-response diagram for each leg.

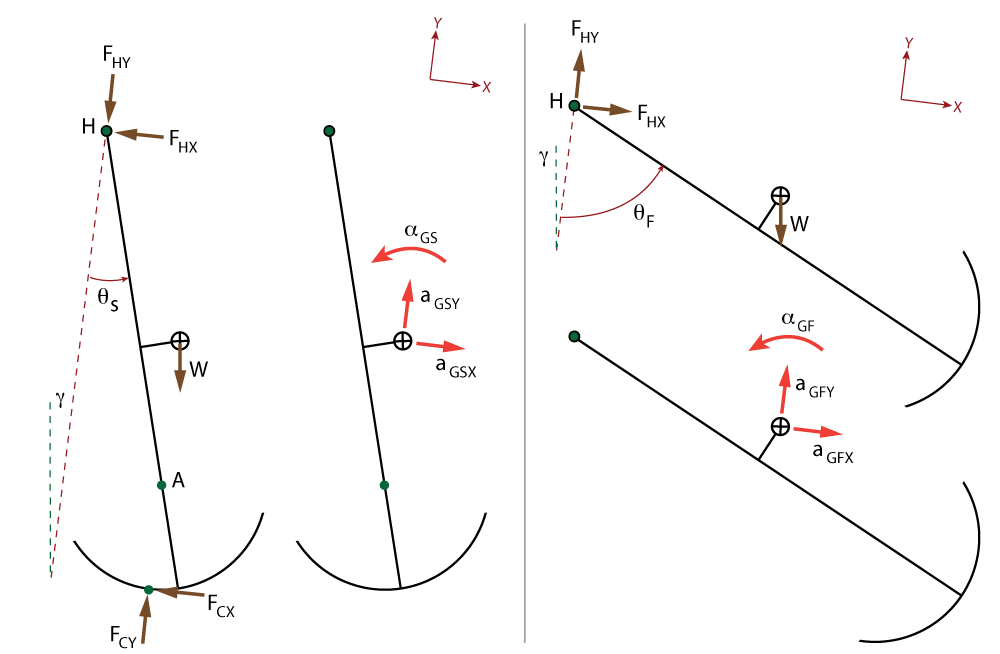
From these, we can generate six equations of motion including ten unknowns (($a_{gsx}$), ($a_{gsy}$), ($\alpha_{gs}$), ($a_{gfx}$), ($a_{gfy}$), ($\alpha_{gf}$), ($F_{cx}$), ($F_{cy}$), ($F_{hx}$), ($F_{hy}$)).


Kinematic Constraints

To solve the system, we must recognize that kinematic constraints exist in our system.

The first of these will arise from the pin joint connecting the two legs. Because each leg is a rigid body, we can relate the hip-joint acceleration to the CG acceleration of each leg

($$\vec{a}_h=\vec{a}_{gs} + \vec{\alpha}_{gs} \times \vec{r}_{h/gs} - \omega_s^2 \; \vec{r}_{h/gs} $$)

($$\vec{a}_h=\vec{a}_{gf} + \vec{\alpha}_{gf} \times \vec{r}_{h/gf} - \omega_s^2 \; \vec{r}_{h/gf} $$)

Which will result in four equations and two more unknowns (($a_{hx}$), ($a_{hy}$)), bringing our total to ten equations and twelve unknowns.

The magic bullet comes from examination of the rolling contact between the stance leg and the ground. Assuming that the leg is rolling without slipping we know the acceleration of both the contact point and center of rotation. Relating these to the acceleration of either the stance-leg CG or the hip will result in two more equations and no more unknowns. With twelve unknowns and twelve total equations, the system should now be solvable!

Heelstrike and Contact Transfer

We will assume that the heelstrike event is perfectly inelastic, and that the force of gravity plays no role during the very short duration of contact transfer. As this means that no torques will be acting on the system, angular momentum of the entire system should be conserved through the heelstrike event. We can also look at just the newly-swinging leg, where we should also be able to apply conservation of angular momentum about the hip joint. In total, these will provide six equations and six unknowns (($v_{gsx}$), ($v_{gsy}$), ($\omega_s$), ($v_{gfx}$), ($v_{fy}$), ($\omega_f$)), allowing one to solve for the post-impact velocity of each leg.