MEAM.Design - MEAM 420 - P1: PUMArt
start: Tuesday, Sept. 29 @ 4:30 p.m.
part 3 deadline: Tuesday, Oct. 6 @ 4:30 p.m.
part 4 deadline: Thursday, Oct. 15 @ 4:30 p.m.
1. Team Formation
Before you will be able to schedule time with the robot, you will need to form a team with two other people. Each team must have at least one graduate student (roughly 1/3 of the class are registered graduate students, so you will likely only have 1 grad student per team). One person from your group must send an email to medesign@seas.upenn.edu with the title “420-P1-team” containing the names of the 3 people who will be working together. This email must be sent before 6:00 p.m. on Wednesday, September 30th. Anyone not included in a team email will be automatically assigned.
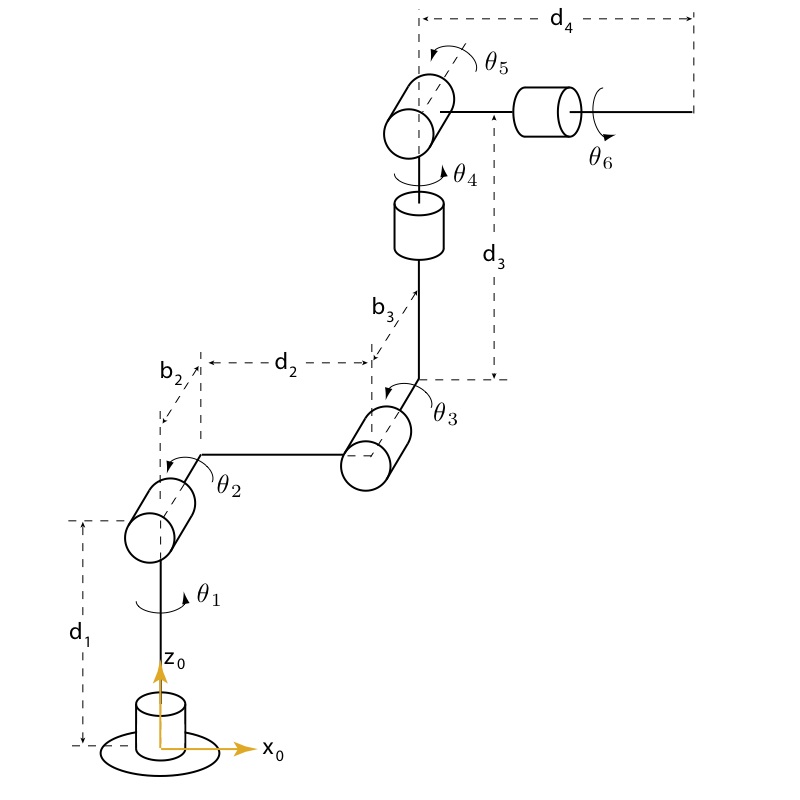
2. Wrist Angles vs. Euler Angles
Given the robot configuration shown to the right, prove to your team that there is a direct mapping between the wrist angles (θ4, θ5, θ6) and the Euler angles (ϕ, θ, ψ) of the end effector (frame 6) with respect to the upper-arm link (frame 3).
3. Full Inverse Kinematics in Matlab
As a group, develop a Matlab function to calculate the six PUMA joint angles when given the position (in millimeters) and Euler angles (in radians) of the end effector with respect to the base (0) coordinate frame. Your code must include a mechanism to handle any singular configurations. The zero configuration of the robot will be as shown in the figure to the right. Zip your Matlab function and any associated scripts together, rename the zip file as "420-P1-XX" (where XX is your team number) and send the zip file as an attachment to medesign@seas.upenn.edu with the title of the email as "420-P1-XX" (where XX is again your team number).
NOTE: ONLY ONCE YOU SUCCESSFULLY COMPLETE PART 3 WILL YOU BE ABLE TO USE THE ACTUAL ROBOT.
4. Lines in Space
A low-level closed-loop PID position controller is operating on each of the joints. To drive the robot to a new position, your code will need to call the function pumaServo(d1,d2,d3,d4,d5,d6), where d is the desired joint angle in radians for each motor, measured from the zero configuration shown above. Develop a Matlab script to drive the end effector of the robot in a straight line within a plane parallel to the x0,y0 plane at a height of 100 mm in z0, while maintaining the wrist pose such that the end effector is pointing straight down (aligned with the -z0 axis).
5. PUMA Art
With a writing instrument mounted to the end effector, use the PUMA to create/draw/write something interesting. You will need to submit your PUMA artwork at the beginning of class on Thursday, October 15th.
Note - our best estimate of actual dimensions and joint limits will be maintained here.