Alejandro Ribeiro | Research / Wireless Control Systems

In this project we want to study networked control systems characterized by the separation of sensing and actuation in different physical devices with control loops incorporating the communication of plant state information over a wireless channel. When sensors and controllers communicate over a wireless channel the cost of controlling the plants gets mixed with the cost of sending plant state information from sensors to controllers. The more information the sensors convey the more precise actuation becomes, but the resulting increase in power consumption at the sensors leads to rapid depletion of its energy resources. It is therefore apparent that a tradeoff emerges between plant performance and power consumption. To quantify this tradeoff we study the problem of selecting plant inputs and power management policies that are jointly optimal with respect to a cost that accounts for plant regulation costs and the costs of conveying information from sensors to controllers.

Figure 1. Wireless control system architecture. The sensor measures plant state $x_k$ and fading channel $h_k$ and transmits with power $p_k$. Messages are decoded at the controller with probability $q_k$ that depends on the channel state $h_k$ and the power $p_k$. We want to find policies that are jointly optimal with respect the aggregate costs of plant regulation and information transmission from sensors to controllers.

A popular alternative to regulate communication cost in wireless control systems is the notion of event triggered control where the idea is to prolong the time elapsed between successive communications by avoiding transmission as long as the plant performance does not deteriorate much. Such triggering of transmissions implicitly reduces the communication cost but transmission expenses are not explicitly accounted. A related approach is to assign a fixed cost to each transmission attempt and proceed to minimize the combination of a control error cost and an aggregate communication penalty. Optimal transmission policies that minimize the aggregate estimation error and communication cost can be characterized using a formulation in terms of infinite horizon Markov decision processes.

Event triggered control and communication penalty formulations are sufficient in some settings but they do not permit the modeling of fading effects neither allow flexibility in the allocation of power to protect some transmissions more than others. Furthermore, it is not possible to incorporate contention effects into either formulation making it difficult to consider cases in which multiple sensors and multiple controllers operate over a shared wireless channel. In this project we model communication cost as the transmitted power at the sensor side. Powers are selected as a function of the plant state and the fading channel realization and affect the likelihood of successful packet decoding through a known complementary error function. The transmitted power is combined with the conventional linear quadratic regulator (LQR) cost to define an aggregate infinite horizon cost that we seek to minimize through proper joint selection of plant and power control policies. Taking advantage of this problem formulation we can mitigate fading through power adaptation to channel conditions and adapt transmitted power to plant conditions so as to, e.g., increase the likelihood of successful packet decoding when the plant state deviates from target. Channel contention is also easily incorporated by modifying the complementary error function to account for packet losses due to simultaneous transmissions.

Single plant over point-to-point channel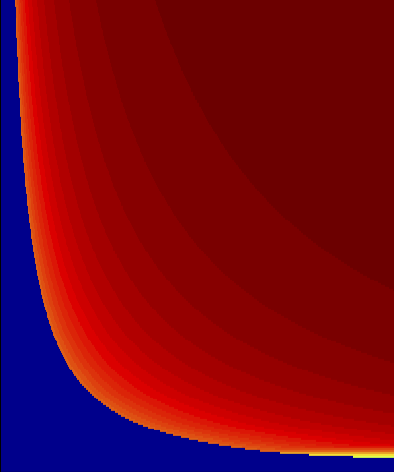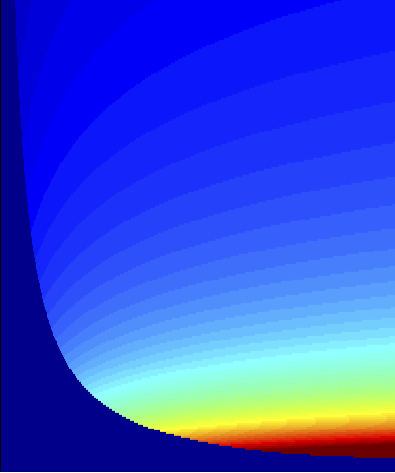

Figure 2. Decoding probability (top) and transmitted power (bottom) as a function of channel (horizontal axis) and plant (vertical axis) states. When channel and state are small the target decoding probability and the transmitted power are zero because transmission is expensive and unnecessary - sowthwest. When both are large target decoding probability is null and transmit power small - northeast. For large channel and small state transmission doesn't help much but is cheap - northwest. For small channel and large plant transmission is expensive but necessary - southeast.

In the context of this project we have begun by studying the (simple) case in which we have a single control loop closed over a point to point channel. The corresponding system architecture is shown in Fig. 1. A sensor measures the plant state $x_k$ and the fading channel state $h_k$ and transmits with power $p_k$. Messages are successfully decoded at the controller with a probability $q_k$ that depends on the channel state $h_k$ and the power $p_k$. If the information is successfully decoded by the controller he learns the current plant state. Otherwise, he propagates past estimates to update his belief on the plant state. In either case a control input $u_k$ is computed and applied to the plant. The goal is to find control inputs $u_k$ and power controls $p_k$ that are good in terms of keeping the state $x_k$ close to target and the power consumption $p_k$ small.

Conceptually, we expect the target successful decoding probability $q_k$ to be close to 1 when the channel and plant state are large and close to zero when they are small. A conceptual colormap of target decoding probability versus channel realization in the horizontal axis and plant state in the vertical axis is shown in Fig. 2-top. When the channel realization is close to zero, successful communication requires investment of a significant amount of power. Thus, the sensor abstains from transmitting unless it is indispensable due to the plant state being far from target - southeast region of the plot. When the channel realization is large transmission is cheap in terms of power and a message is sent even if the plant is close to target - northwest region of the plot. When the channel realization as well as the plant state are large, the target decoding probability is close to 1 because it is both, cheap and necessary - northeast region of the plot. When channel and state are small the target decoding probability is zero because transmission is expensive and unnecessary - sowthwest region of the plot.

The corresponding conceptual power map is shown in Fig. 2-bottom. When channel and state are small the transmitted power are zero because transmission is expensive and unnecessary - sowthwest region go the plot. When both are large a small amount of power is invested to yield a large decoding probability that is instrumental in bringing the plant closer to target - northeast region go the plot. For large channel and small state transmission doesn't help much but is cheap and a small amount of power is invested in a transmission attempt - northwest region go the plot. When the channel realization is small and the plant is far from traget transmission is expensive but necessary resulting in the investment of a significant amount of power in the transmission attempt - southeast region go the plot.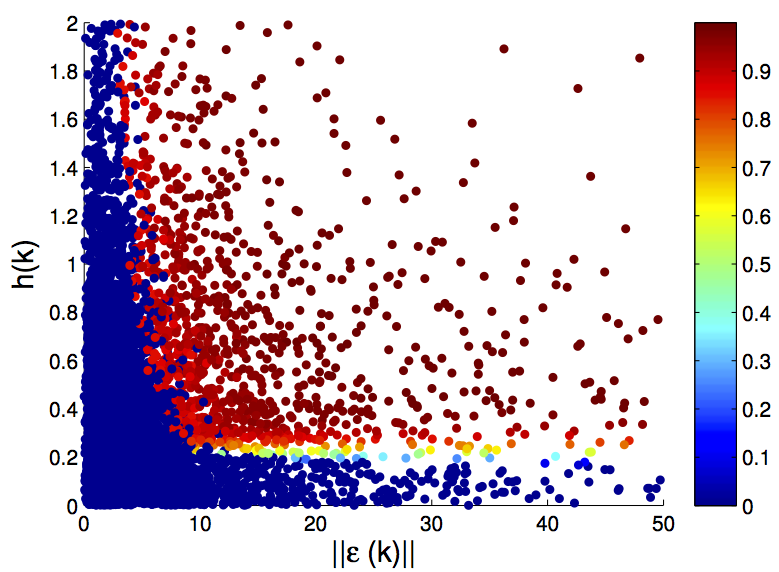

Figure 3. Power allocation of a rollout policy for joint optimization of control inputs and transmitted power. Allocated power is consistent with the conceptual plot in Fig. 2-bottom.

The conceptual allocation in Fig. 3 has been corroborated by our analysis and algorithmic development. We have identified a restricted information structure that permits decoupling of optimal plant and power control policies. For this particular information structure the usual LQR control law becomes optimal at the controller side while the optimal communication policy follows from a Markov decision process (MDP) formulation involving transmitted power and the state estimation error at the controller side. We then leverage this separation principle to express optimal power control policies in terms of a value function. While this does not allow computation of optimal policies it does allow us to understand their qualitative properties. These qualitative properties are the source of the target decoding probability map in Fig. 3 and the transmitted power map in Fig. 3. We can think of the event-triggered paradigm as a special case in our formulation, where instead of deciding how much power to allocate to the transmission attempt we just decide whether to transmit or not. This interpretation is fostered by the realization that conventional event triggered policies emerge as the optimal communication strategy if the sensor uses capacity achieving forward error correcting codes. We have also derived suboptimal power control policies using a rollout algorithm. Numerical simulations of this algorithm yield power allocations like the one shown in Fig. 3, which is consistent with the conceptual plot in Fig. 2-bottom.

Ongoing work, acknowledgements, and references

Most of our current effort is centered on developing generalizations where there are multiple sensors and controllers sharing a common wireless channel. We are considering different contention protocols which give rise to different policies to manage channel scheduling along with power allocation and plant control policies. We are also working on alternative formulations where we account not only for the transmitted power at the sensor but also by standby power consumption at the receiver and transmitter ends. In this case sleeping becomes important and leads to policies where sleeping times needs to be prearranged based on beliefs about the evolution of the plant state.

This is the Ph.D. work of Konstantinos Gatsis. We also count on the substantial expertise of Dr. Miroslav Pajic and Prof. George Pappas. The list of publications resulting from this project is the following:

bibtexsummary:[01_my_journals_2012.bib,GatsisEtal13]
bibtexsummary:[02_my_conferences_2013.bib,cGatsisEtal13]

If you want to understand our work here, the journal paper submission [1] is the place to start. The conference paper [2] is an abridged version of [1] and is a finalist for the best student paper award the 2013 American Control Conference (ACC).