|
Research /
Communication networks for autonomous robot teamsThe confluence of advances in robotics and wireless communications has led to the emergence of autonomous robot teams that cooperate to accomplish tasks assigned by human operators. A typical scenario is search and rescue missions in hazardous situations where a team is deployed to scout points of interest. While a designated lead member of the team moves to a specified location, the remaining robots provide mission support. Critical for task accomplishment is the availability of wireless communications. Communication is required to exchange information between robots as well as to relay information to and from the human operators. Availability of wireless communication infrastructure, however, is unlikely in the harsh environments in which autonomous robot teams are to be deployed. Rather, we want the robots to self organize into a wireless network capable of supporting the necessary information exchanges. The goal of this project is to design cyber-physical controllers that determine (physical) trajectories for the robots while ensuring (cyber) availability of communication resources. 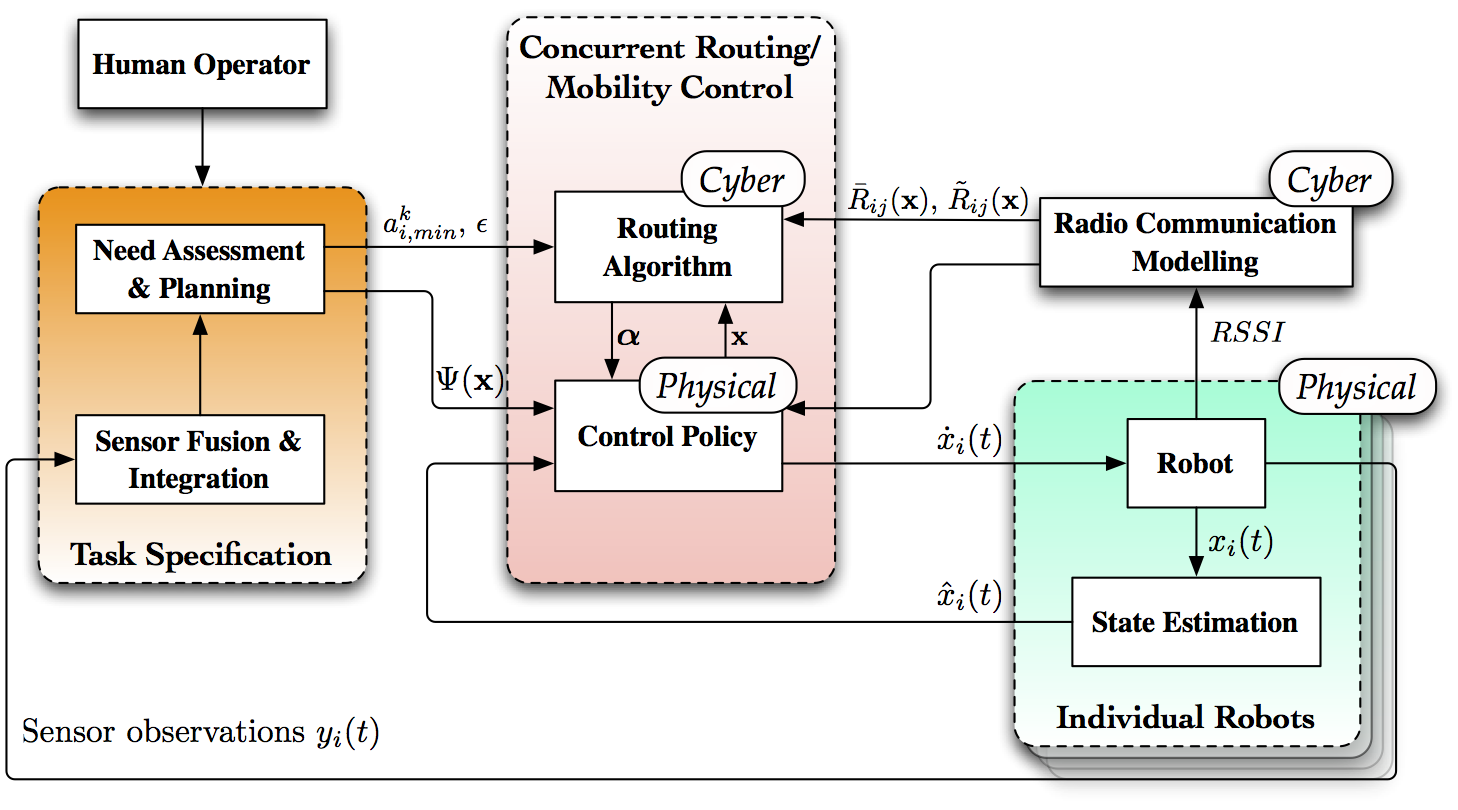 Figure 1. System architecture for joint control of mobility and routing. Task Specification here represents a generic spatial application defined by a convex task potential function $\Psi(x)$ while providing a stream of data to the human operator. Individual robot components consist of the low-level robot control, estimation, and communication. We additionally assume that a subsystem is available to build an online model of radio communication in the environment. The focus of this work is on developing concurrent methods for routing and mobility control. The fundamental roadblock to guaranteeing reliable communication is the unpredictability of wireless propagation. The cluttered environments in which robot teams are to be deployed are characterized by severe fading resulting in volatile communications performance even for short distance communications. Channel strength variations in the order of 10 to 20 dB are typical when robots move a distance comparable to the radio wavelength – for reference, the wavelength is 30 cm for communications in the 800MHz band. This drawback notwithstanding, it has to be noted that the goal of the self-organized network is to maintain reliable end-to-end communication between, say, the lead member of the scouting team and the operation base. We can then exploit spatial redundancy across channels to minimize the effect of point-to-point uncertainty in end-to-end communication rates. By splitting traffic flows between various neighboring robots, we ensure that while failure of a particular link may reduce end-to-end communication rates, it does not interrupt them completely. To realize this idea we adopt a stochastic model of connectivity in which achievable point-to-point rates are random quantities with known mean and variance. If point-to-point rates are random, end-to-end rates are also random. The cyber part of our control algorithms assume given positions and determine routing variables that minimize the probability of end-to-end rates falling below a minimum level of service. The physical control block determines robot trajectories that are restricted to configurations that ensure these probabilities stay above a minimum reliability level. (:quicktime http://www.seas.upenn.edu/~aribeiro/videos/robust_routing_levine.mov width=500 height=300 scale=0.4 autoplay=off:) Figure 2. Proof of concept for joint control of mobility and routing in autonomous robot teams. An architecture diagram is shown in Fig. 1. As with any mobility control system, there is a block performing task specification, a second block executing the control law, and a third block conducting actuation and state estimation. The task specification block interfaces with the human operators and integrates robot observations and requirements to determine specifications that it passes on to the control block. These specifications come in the form of a potential function $\Psi(x)$ that must be minimized and communication rates $a_{i,\min}^k$ that must be maintained at all times. The control block then determines control inputs $\dot x(t)$ and network variables $\alpha(t)$ that are conducive to task completion. Individual robots implement the control law $\dot x(t)$ and route packets according to variables $\alpha(t)$. Robots also take observations $y_i(t)$, e.g., a video feed, that they relay to task planning and perform position estimation $\hat{x}_i(t)$ that they feedback to the control block. Using available technologies for mapping, control, and state estimation, each robot estimates its position $\hat{x}_i(t)$ and controls its velocity $\dot x_i(t)$ with respect to a common known map of the environment. The control algorithm also necessitates access to achievable rates $R_{ij}(x)$ which are provided by a radio communication modeling block. Our work is concerned, for the most part, with the joint selection of suitable communication variables $\alpha(t)$ and path plans $x(t)$. Our work is concerned, for the most part, with the joint control of mobility and routing In the context of this project we have developed algorithms that rely on the computation of communication routes and trajectories by a central command center. The plans are then communicated to the individual robots that proceed to implement the plan. A proof of concept of the overall system is shown in the video in Figure 2. Our current effort focuses on the development of distributed algorithms and further experimental validation. Decentralized communications protocolsTo avoid the computation of routes at a centralized location we are developing algorithms to determine optimal robust routes in a distributed manner. Robots are supposed to have access to local channel information and the ability to communicate with nearby robots but are unaware of the network's topology beyond their local neighborhood. Using local information and variable exchanges between neighbors we devise iterative protocols that determine optimal routing policies as times grows. A common approach to devise distributed optimal routing algorithms is to implement gradient descent in the dual function of the corresponding optimization problem – or subgradient descent if the dual function is nondifferentiable. Optimal routing problems include a maximization objective that determines the metric used to compare different configurations as well as constraints that determine feasible routing variables. To formulate the dual problem we introduce Lagrange multipliers associated with each of the constraints and proceed to find configurations that optimize the linear combination of objective and constraints that they define. The dual problem corresponds to the determination of multipliers that render the constrained optimization and the linear combination optimization equivalent. The important property of the dual function that makes it appealing to distributed implementations is that it is possible to compute gradients of the dual function in a distributed manner. Robots maintain local routing variables and local multipliers used to enforce their local routing constraints. They then proceed to recursively update primal variables by finding optimal routes for given duals and dual variables by performing a gradient descent step. The first fundamental observation is that dual gradients can be found as the constraint slack associated with the optimal routing configuration. The second fundamental observation is that all of the required computations can be implemented in a distributed manner. Determination of optimal routes requires access to local and neighboring dual variables whereas dual gradients are given as functions of local and neighboring multipliers. Decentralized motion planningFor fully autonomous operation, decentralized networking protocols need to be integrated into decentralized motion planning algorithms. Our networking protocols determine routing variables that maximize the probability of survival of end-to-end communication flows. However, for some spatial configurations it is impossible to maintain these probabilities above a minimum target level. Since the likelihood of network survival for those configurations is not sufficient for mission requirements, these spatial arrangements generate a virtual obstacle in configuration space. The purpose of this task is to design decentralized reactive as well as deliberative planners to steer system configurations away from the virtual obstacle region created by network survivability requirements. In the context of reactive planners the solution involves the incorporation of barrier potentials to avoid crossing into the infeasible space. The key research issue to be addressed here is the integration of the decentralized algorithm for optimal communication with the decentralized version of motion planning. For the development of distributed deliberative planning algorithms the challenge is to let robots make consistent local plans based on perceptions of their different local environments. Robots may know the position of some nearby peers and have good estimates of the communication channels that link them. For some more distant agents this knowledge becomes more uncertain and may even become unavailable for some robots. The foremost difficulty is not the uncertain knowledge but the fact that network state information is different at different robots. Our objective is to determine optimal trajectories that take into account the fact that different terminals have different beliefs on the network state and are bound to select conflicting actions. The resolution of conflicting actions leads naturally to the use of controllers based on partially observable Markov Decision Processes (POMDP). POMDPs provide a general decision making framework for acting optimally in partially observable domains. In lieu of deterministic state estimates the system's state is described in information space where probability distributions on robots' positions and channels are maintained. Planning decisions are then made to maximize a discounted expected payoff across all possible paths. In a distributed context each robot plans a joint optimal trajectory based on its local belief and proceeds to move according to this plan. Since different robots have different beliefs the actual joint trajectory is different from local beliefs. Upon observation of these different trajectories robots update their local beliefs and repeat the process. The advantage of a POMDP formulation is that it is easy to incorporate probabilistic safety constraints to reduce the likelihood of finding the team in spatial configurations for which it is impossible to guarantee network connectivity. Acknowledgments and referencesThis project got started on collaboration with Dr. Jon Fink, who is now at the Army Research Lab. The work on decentralized algorithms got started on a collaboration with Prof. Mihalis Zavlanos, who is now at Duke University. We also collaborated with Jon's and Mihalis's respective advisors, Prof. Vijay Kumar and Prof. George Pappas. Currently, this project is the Ph.D. work of James Stephan. The following is a list of papers produced in the context of this project:
The framework described here is presented in the journal publications [1] and [3]. The work in [3] is more tutorial in nature. Many details are omitted and those are discussed in [1]. A comprehensive presentation of our work on distributed implementations is available in [1]. The conference papers [4] and [7] are preliminary versions of [1] and [3]. The conference papers [5], [6], and [8] are preliminary versions of [2]. |