|
Research /
Distributed optimizationIn distributed optimization problems agents want to find local variables that are optimal with respect to a local utility while satisfying linear coupling constraints with variables of neighboring nodes. For a more precise definition consider a network composed of $N$ nodes indexed by $i$ and denote as $n(i)$ the set of neighbors of $i$ and as $\mathbf{C}$ the directed edge incidence matrix of the graph. Each of the nodes keeps track of a local variable $x_i$ and a local concave utility function $f_i(x_i)$. We want to select variables that maximize the sum utility $\sum_i f_i(x_i)$ subject to the requirement that the variables $x_i$ are such that $x_i = x_j$ for all nodes $j\in n(i)$ in its neighborhood. For a connected network this is the same as requiring that the variables $x_i$ have the same value for all nodes and this particular problem formulation is therefore termed a consensus optimization problem. Defining the vector $\mathbf{x}=[x_1,\ldots,x_N]^T$ grouping all local variables and letting $\mathbf{0}$ be the all-zero vector of proper dimension we can write the consensus optimization problem as $\mathbf{x}^* = $ argmax $ \sum_i f_i(x_i),$ subject to $\mathbf{C} ^T \mathbf{x} = \mathbf{0}.$ 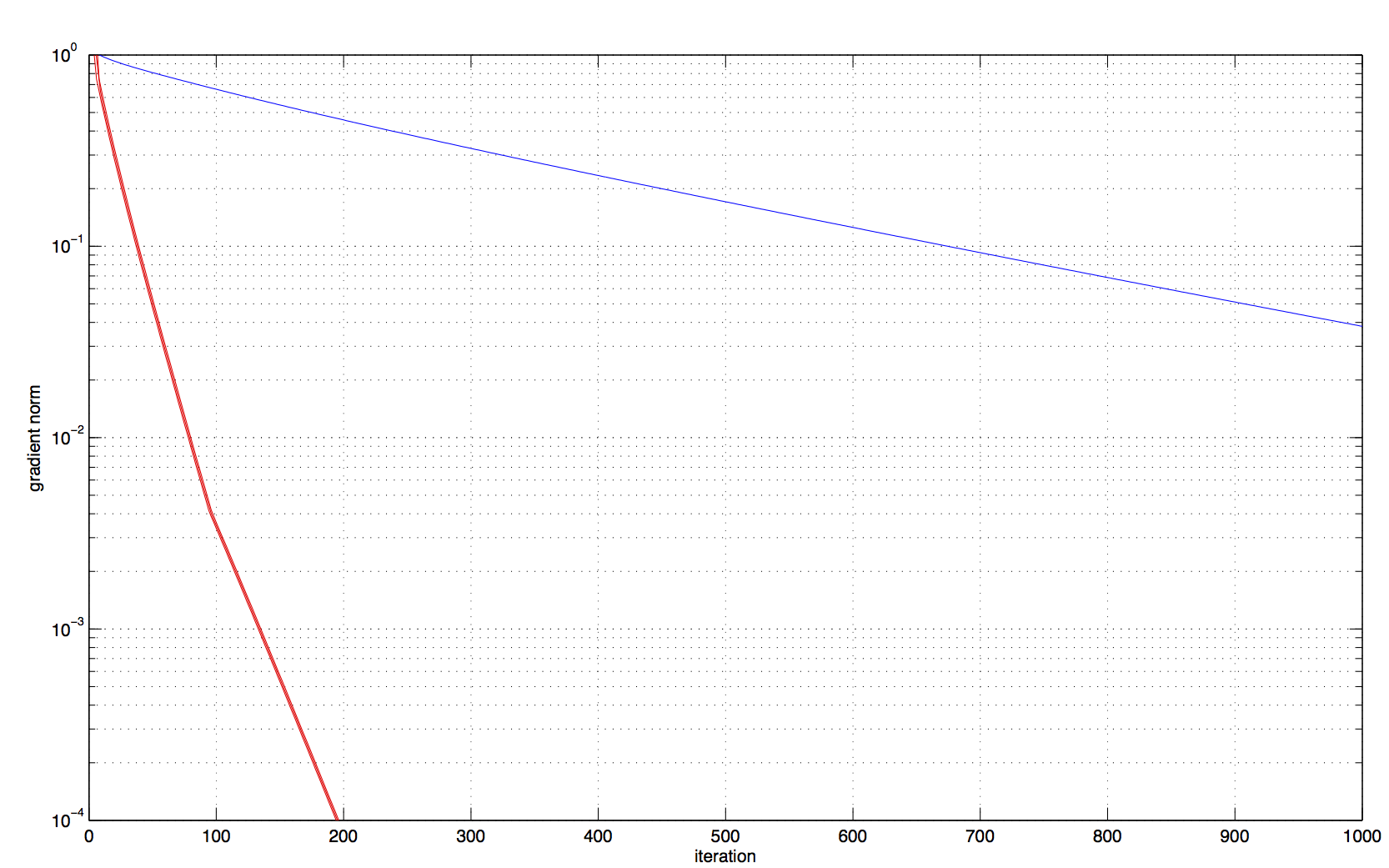 Figure 1. Infinity norm distance from primal iterates to optimal arguments for ADD-1 (red) and ADMM (blue). The curvature correction of ADD retains reasonable convergence times for problems that are not well conditioned. (Directed cycle network with 50 nodes and 50 random edges. Quadratic primal objectives with condition number 10.) A particular application of a consensus optimization problem is distributed maximum likelihood estimation. In such case the variables $x_i$ take the place of a local estimate, the functions $ f_i(x_i)$ represent local log likelihoods determined by local observations, and the goal is for each agent to compute a local estimate using global information. Another important application can be obtained by replacing the matrix $\mathbf{C}$ in the equation above to model optimal flow problems. Regardless of the particular application it is of interest to derive distributed optimization algorithms to solve distributed optimization problems. These algorithms rely on iterative computation of candidate solutions $x_i(t)$ and variable exchanges between neighboring nodes so that as time progresses the iterates $x_i(t)$ approach the optimal variable $x_i^*$. The original use of distributed optimization algorithms was for distributed control and information aggregation in wireless sensor networks. Currently, there is renewed interest in these algorithms as per their applicability to solve massive dimensional optimization problems in server clusters. In the latter setting there is interest in subdividing the optimization problem into separate servers while keeping communication requirements subdued. There are different approaches that lead to distributed optimization algorithms. Our work concentrates on methods that operate in the dual domain. Without digressing into technical details the structure of the dual function is such that it is possible to compute gradients of the dual function in a distributed manner. These gradients can then be used to implement a dual gradient descent algorithm that converges toward the optimal dual variables from which the optimal primal variables of the optimization problem introduced above can be recovered as a byproduct. Dual gradient descent algorithms are valuable for their simplicity but their application is limited to problems whose dual functions are well conditioned. Since the condition number of the dual function is roughly given by the product of the condition number of the primal function and the ratio between the largest and smallest eigenvalues of the graph's Laplacian, this requires tame networks and primal functions. Tame primal functions are those with good condition numbers. Tame networks are those that have small diameter and some form of regularity on the number of connections per node. 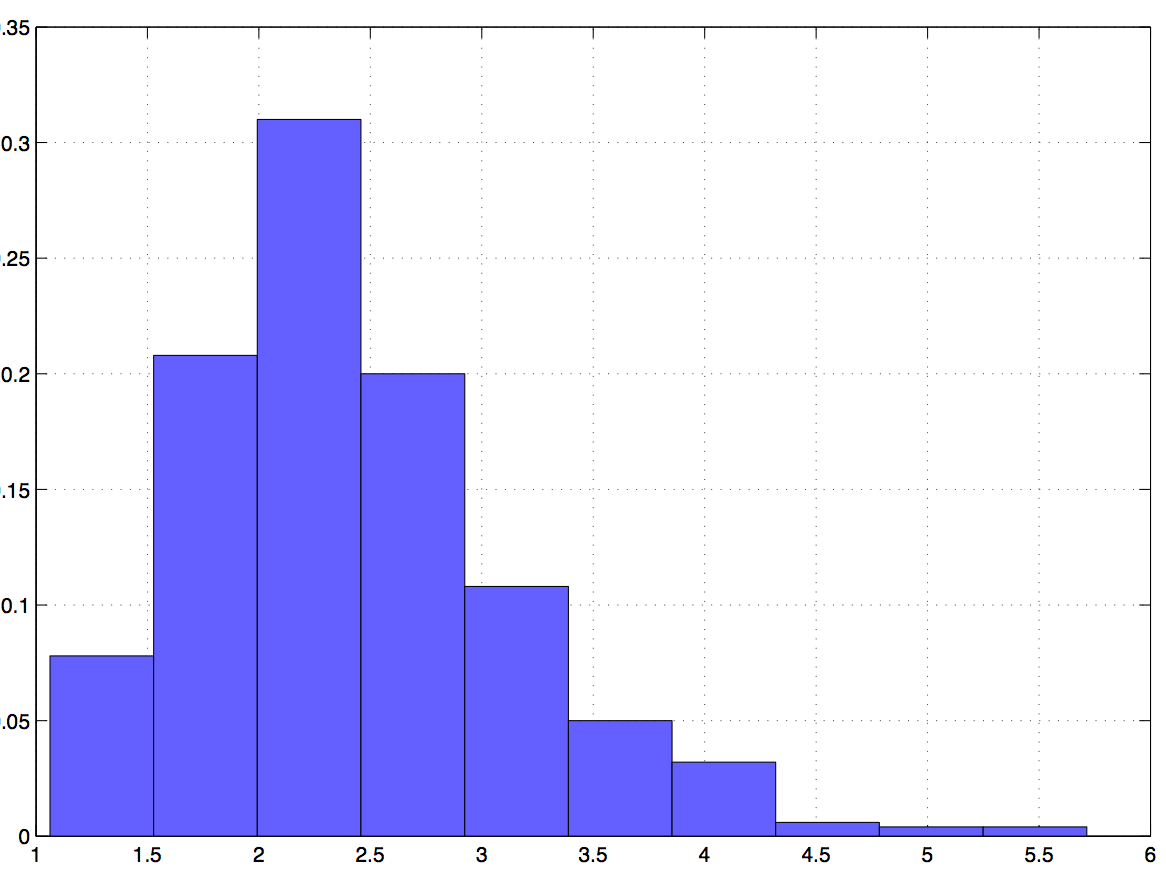 Figure 2. Relative convergence times of ADMM with respect to ADD-1 for a well conditioned problem. Convergence times are similar since ADD's curvature correction is of little help in a problem that already has a tractable shape. (Directed cycle network with 20 nodes and 40 random edges. Quadratic primal objectives with condition number 1. Time to reach infinity norm distance $10^{-4}$ to optimal arguments) A similar algorithm with better convergence properties is the Alternating Direction Method of Multipliers (ADMM) which is based on the addition of a quadratic regularization term to the the problem's Lagrangian. The ADMM is less sensitive to the condition of the dual function. It's performance still degrades with increasing condition number but the degradation is much smaller than the degradation corresponding to dual gradient descent. Whereas dual descent is all but impractical for problems having more than a few nodes and condition numbers not close to one, ADMM is slow but acceptable for problems with moderate number of nodes and moderate condition numbers. A convergence rate illustration is shown in Fig. 1 that depicts the infinity norm distance between ADMM iterates and the primal optimal argument $\mathbf{x}^*$. The network is a directed cycle graph with 50 nodes to which 50 random edges have been added. The primal objective is a quadratic function with condition number 10. A distance to optimality of about $4\times10^{-2}$ is attained in $10^3$ iterations. While better behaved than dual descent, convergence of ADMM is still inadequate and can be made arbitrarily slow by increasing the condition number of the primal function or modifying the network to increase the ratio between the largest and smallest eigenvalue of the graph's Laplacian. Ultimately, this drawback can only be corrected by implementing curvature corrections as in Newton and quasi-Newton methods. Our research on this project is concerned with the development of distributed optimization methodologies that emulate Newton's method as a means of attaining quadratic convergence rates. We discuss these methods in the following section but a preliminary simulation is shown in shown in Fig. 1 depicting the infinity norm distance between iterates obtained by our distributed optimization methods and the primal optimal argument $\mathbf{x}^*$. For the same problem parameters used for ADMM, we converge to distance $10^{-2}$ in less than 100 iterations and to distance $10^{-4}$ in 200 iterations. Accelerated dual descentThe natural alternative to accelerate convergence rate of first order gradient descent methods is to use second order Newton methods, but these methods cannot be implemented in a distributed manner. Indeed, since (centralized) implementation of the Newton method necessitates computation of the inverse of the dual Hessian, it follows that a distributed implementation would require each node to have access to a corresponding row of this inverse Hessian. It is not difficult to see that the dual Hessian is in fact a weighted version of the network’s Laplacian and that as a consequence its rows could be locally computed through information exchanges with neighboring nodes. Its inversion, however, requires global information. 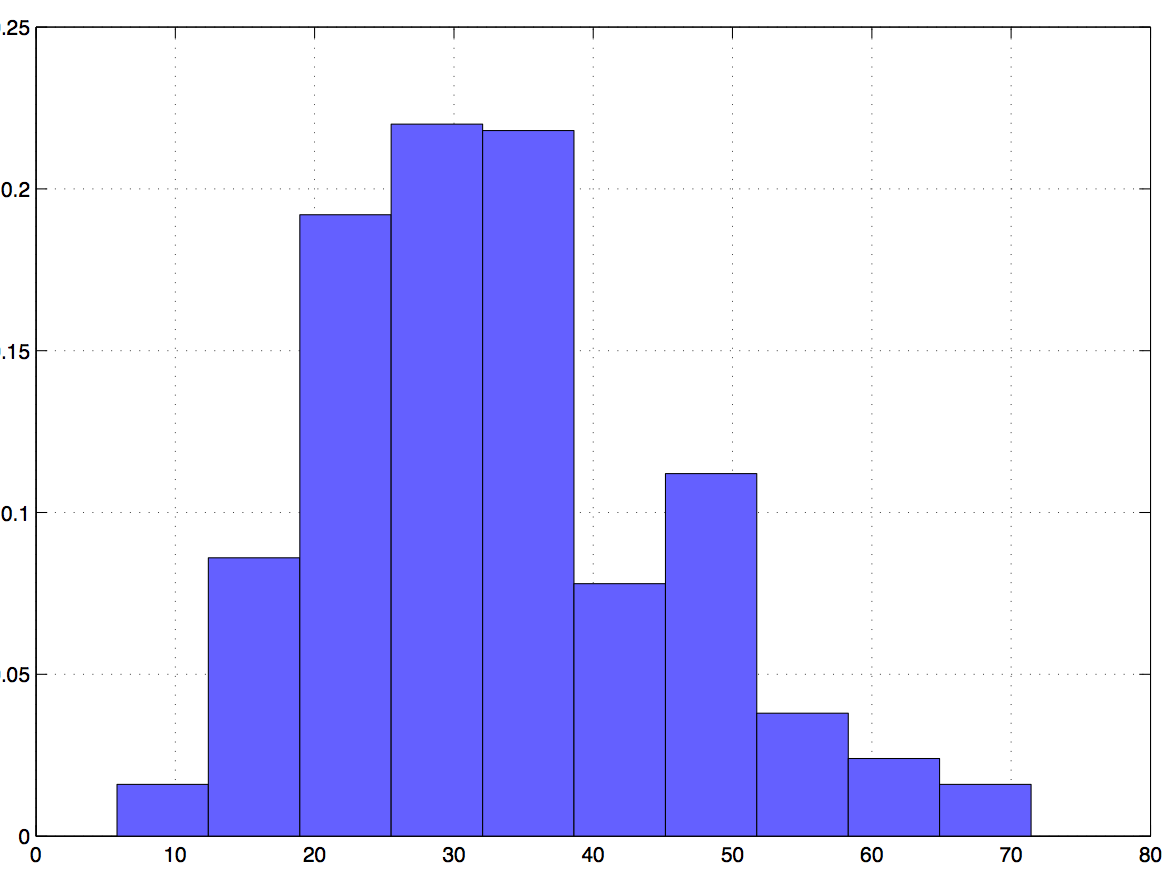 Figure 3. Relative convergence times of ADMM with respect to ADD-1 for an ill conditioned problem. Convergence times are more than one order of magnitude faster for ADD. The curvature correction is essential to achieve reasonable convergence times. (Quadratic primal objectives with condition number 1. Other parameters as in Fig. 2.) The insight at the core of this research thrust is to consider a Taylor's expansion of the inverse Hessian which, being a polynomial with the Hessian matrix as variable, can be implemented through local information exchanges. More precisely, considering only the zeroth order term in the Taylor's expansion yields an approximation to the Hessian inverse based on local information only. The first order approximation necessitates information available at neighboring nodes and in general, the $N$th order approximation necessitates information from nodes located $N$ hops away. The resultant family of Accelerated Dual Descent (ADD) algorithms permits a tradeoff between accurate Hessian approximation and communication cost. We use ADD-$N$ to represent the $N$ th member of the ADD family. ADD-$N$ uses the $N$th order Taylor approximation of the Hessian inverse by collecting information from terminals $N$ hops away. Our research on ADD has shown that convergence of algorithms in the ADD family follows three distinct phases. The behavior during the first phase is defined by an approximate backtracking line search which ensures a constant decrease towards the optimal objective. During the second phase ADD-N algorithms exhibit quadratic convergence despite the fact that they rely on approximate Newton directions. In the third and terminal phase convergence slows down to linear as errors in the Newton step become comparable to the step’s magnitude. The first two phases are akin to the linear and quadratic phases of Newton algorithms. The transition between the second and third phase can be delayed by increasing $N$, although this may result in increased overall communication cost. Our numerical studies corroborate substantial imporvements in convergence times. Fig. 2 shows the ratio of times required by ADMM and ADD-1 to reach an infinity norm distance to the optimal arguments of at least $10^{-4}$ for a primal quadratic objective with condition number 1 in a directed cycle network with 20 nodes to which 40 random edges have been added. Since the curvature of the original problem is benign both methods exhibit similar convergence rates. Modifying the objective to yield a condition number of 10 results in convergence times for ADD-1 that are 20 times faster than the convergence times of ADMM as we show in Fig. \ref{fig_no_ill_conditioned}. Our current work includes extensions of ADD to problems with dual functions that have singular Hessians and that are not differentiable at all times. We are also considering to stochastic optimization problems and alternative approaches based on different matrix splittings and quasi-Newton methods. We also have a parallel research project in which we consider dynamic optimization problems characterized by time varying objectives. In the latter case the challenge is that in the time it takes for iterative algorithms to converge to the optimal argument the objective has changed enough for the optimal operating point to be different. Acknowledgments and referencesMy work on distributed optimization got started on a collaboration with Prof. Ioannis Schizas and Prof. Georgios Giannakis where we adapted the ADMM to solve distributed maximum likelihood estimation problems. As an aside note, observe that while interest in the ADMM for distributed network optimization has been revived by an excellent tutorial manuscript by Boyd et al., it is Ioannis Schizas who deserves credit for adopting the ADMM as a tool for solving distributed consensus optimization problems. This paper predates Boyd et al. by a good three years and spawned a literature of a couple hundred papers dealing with various applications. The Accelerated Dual Descent (ADD) family of algorithms is the Ph.D. work of Mike Zargham in collaboration with Prof. Ali Jadbabie, Prof. Asuman Ozdaglar, and myself. The list of papers related to this work is the following:
The development of the ADD family is presented in the journal paper [1]. Conference papers [3] and [4] contain preliminary abridged versions of the material that went into the preparation of [1]. Conference submission [2] is a preliminary report on the use of ADD for stochastic optimization problems. The somewhat parallel work on dynamic distributed optimization is part of the Ph.D. work of Felicia Jakubiec. During a visit to Penn, Qing Ling from the University of Science and Technology of China (USTC) has contributed his invaluable expertise. Our work on this topic has appeared here:
Our work on dynamic optimization is covered in the journal submission [1]. Conference papers [2] and [3] are abridged versions of [1]. |