Alejandro Ribeiro | Research / Bayesian network games

In many situations agents in a network want to take actions that are optimal with respect to an unknown state of the world and the actions taken by other agents in the network who themselves are trying to select actions that are optimal in the same sense. In, e.g., trade decisions in a stock market, the payoff that a player receives depends not only on the fundamental (unknown) price of the stock but on the buy decisions of other market participants. After all, the price of a stock moves up as long as it is in high demand, which may or may not be because of sound fundamentals. In such situations players must respond to both, their belief on the price of the stock and their belief on the actions of other players. Similar games can also be used to model the coordination of members of an autonomous team whereby agents want to select an action that is jointly optimal but only have partial knowledge about what the action of other members of the team will be. Consequently, agents select actions that they deem optimal given what they know about the task they want to accomplish and the actions they expect other agents to take.

In both of the examples in the previous paragraph we have a network of autonomous agents intent on selecting actions that maximize local utilities that depend on an unknown state of the world -- information externalities -- and the also unknown actions of all other agents -- payoff externalities. In a Bayesian setting -- or a rational setting, to use the nomenclature common in the economics literature -- nodes form a belief on the actions of their peers and select an action that maximizes the expected payoff with respect to those beliefs. In turn, forming these beliefs requires that each network element make a model of how other members will respond to their local beliefs. The natural assumption is that they exhibit the same behavior, namely that they are also maximizing their expected payoffs with respect to a model of other nodes' responses. But that means the first network element needs a model of other agents' models which shall include their models of his model of their model and so on. The fixed point of this iterative chain of reasoning is a Bayesian Nash Equilibrium.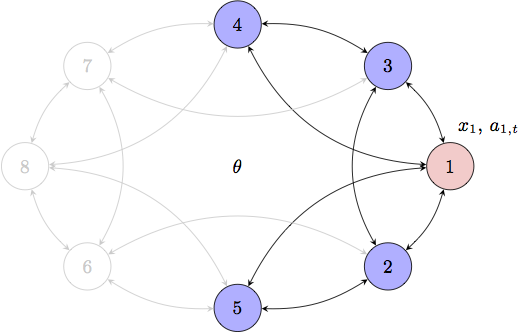

Figure 1. Bayesian network game. Agents want to select actions that are optimal with respect to an unknown state of the world and the actions taken by other agents. We consider repeated versions of this game in which agents observe the actions taken by neighboring agents at a given time.

In this project we consider repeated versions of this game in which agents observe the actions taken by neighboring agents at a given time. In observing neighboring actions agents have the opportunity to learn about the private information that neighbors are, perhaps unwillingly, revealing. Acquiring this information alters agents' beliefs leading to the selection of new actions which become known at the next play prompting further reevaluation of beliefs and corresponding actions. In this context we talk of Bayesian learning because the agents' goal can be reinterpreted as the eventual learning of peers' actions so that expected payoffs coincide with actual payoffs. A schematic representation of this model is shown in Fig. 1. The payoff at time $t$ of, say, agent 1 depends on the state of the world $\theta$ and the actions $a_{i,t}$ of all other agents. At the initial stage of the game, agent 1 has access to a private signal $x_1$ which he uses to select the action $a_{1,1}$. It then takes this action and simultaneously observes the actions $a_{i,1}$ of agents in its neighborhood, i.e., $i=1,3,4,5$. These observed actions reveal further information about $\theta$ and the actions that are to be taken by other agents at time $t=2$. This prompts selection of a likely different action $a_{1,2}$. Observation of actions $a_{i,2}$ of neighboring agents reveals further information on the world state and actions of other players and prompts further reevaluation of the action to be taken at the subsequent stage.

This project involves two relatively separate thrusts respectively concerned with the asymptotic properties of the Bayesian Nash Equilibria and with the development of algorithms that agents can use to compute their equilibrium actions. The former thrust is conceptual and mostly of interest as a model of human behavior in social and economic networks. The latter thrust is of interest to enable the use of network games as distributed algorithms to plan the actions of members of an autonomous team.

Asymptotic learning

As mentioned earlier we can reinterpret an agent's purpose as the eventual learning of all available information about the state of the world and the peers' actions. The question we try to answer in this thrust is whether this information is eventually learnt or not.

Different behavioral assumptions lead to different outcomes. In particular, the way agents revise their views in face of new information and the actions they choose given these views determines the long run outcome of the game. In our preliminary work we assume that agents are myopic in that they choose actions at each stage of the game which maximize their stage payoffs, without regard for the effect of these actions on their future payoffs. We use this behavioral assumption to prove formal results regarding the agents’ asymptotic equilibrium behavior. Our analysis yields several interesting results. First, agents’ actions asymptotically converge for almost all realizations of the game. Furthermore, given a connected observation network, agents’ actions converge to the same value. In other words, agents eventually coordinate on the same action. Second, agents reach consensus in their best estimates of the underlying parameter. Finally, if some agent can eventually observe her own realized payoffs, agents coordinate on an action which is optimal given the information dispersed among them. This result suggests that in a coordination game -- where agents’ interests are aligned -- repeated interactions between agents who are selfish and myopic could eventually lead them to coordinate on the socially optimal outcome.

We are currently investigating further properties of steady state equilibrium plays for Bayesian games with myopic players. We are also looking into networks with non-myopic players and relaxing assumptions on the knowledge of network topology and other structural information.

Quadratic network game filter

The burden of computing a Bayesian Nash equilirium in repeated games is, in general, overwhelming even for small sized networks. This intractability has led to the study of simplified models in which agents are non-Bayesian and update their beliefs according to some heuristic rule. A different simplification is obtained in models with pure information externalities where payoffs depend on the self action and an underlying state but not on the actions of others. This is reminiscent of distributed estimation since agents deduce the state of the world by observing neighboring actions without strategic considerations on the actions of peers. Computations are still intractable in the case of pure information externalities and for the most part only asymptotic analyses of learning dynamics with rational agents are possible. Explicit methods to maximize expected payoffs given all past observations of neighboring actions are available only when signals are Gaussian or when the network structure is a tree. For the network games considered in this project in which there are information as well as payoff externalities, not much is known besides the asymptotic analyses of learning dynamics described above.This is an important drawback for the application of network games to the implementation of distributed actions in autonomous teams. The purpose of this thrust is to develop algorithms to enable computation of equilibrium actions.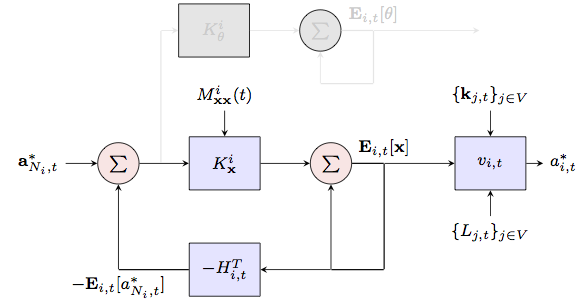

Figure 2. Quadratic Network Game (QNG) filter. Agents tun the QNG filter to compute Bayesian Nash equilibrium actions in games with quadrate payoffs and Gaussian private signals.

Our first result considers payoffs represented by a utility function that is quadratic in the actions of all agents and an unknown parameter. At the start of the game each agent makes a private observation of the unknown parameter corrupted by additive Gaussian noise. To determine a mechanism to calculate equilibrium actions we introduce an outside clairvoyant observer that knows all private observations. For this clairvoyant observer the trajectory of the game is completely determined but individual agents operate by forming a belief on the private signals of other agents. We start from the assumption that this probability distribution is normal with an expectation that, from the perspective of the outside observer, can be written as a linear combination of the actual private signals. If such is the case we can prove that there exists a set of linear equations that can be solved to obtain actions that are linear combinations of estimates of private signals. This result is then used to show that after observing the actions of their respective adjacent peers the probability distributions on private signals of all agents remain Gaussian with expectations that are still linear combinations of the actual private signals. We proceed to close a complete induction loop to derive a recursive expression that the outside clairvoyant observer can use to compute BNE actions for all game stages. We then leverage this recursion to derive the Quadratic Network Game (QNG) filter that agents can run locally, i.e., without access to all private signals, to compute their equilibrium actions. A schematic representation of the QNG filter is shown in Fig. 2 to emphasize the parallelism with the Kalman filter. The difference is in the computation of the filter coefficients which require the solution of a system of linear equations that incorporates the belief on the actions to be taken by other agents.

Our current research program includes developing analogues of the QNG filter for different network types and leveraging the QNG filter to solve games where payoffs are not quadratic and private signals are not Gaussian. The similarity with Kalman filters is instrumental here as it points out to the existence of filters akin to extended or unscented Kalman filters as well as particle filters.

Acknowledgments and references

This is the Ph.D. work of Ceyhun Eksin and Pooya Molavi. We also count on invaluable help from Ali Jadbabie. The list of publications resulting from this project is the following:

bibtexsummary:[01_my_journals_2013.bib,EksinEtal13a]
bibtexsummary:[01_my_journals_2013.bib,EksinEtal13]
bibtexsummary:[02_my_conferences_2013.bib,cEksinEtal13]
bibtexsummary:[02_my_conferences_2012.bib,cEksinEtal12a]
bibtexsummary:[02_my_conferences_2012.bib,cEksinEtal12]

To understand this project the best place to start is the tutorial article [1] which appeared in the Signal Processing Magazine. For complete details on the QNG filter the journal submission [2] os the best place to start. The conference submission in [3] is an abridged version of the journal paper [2]. Conference submissions [4] and [5] contain our results on asymptotic learning.