|
Research /
Circles of trust: Hierarchical clustering in asymmetric networksMiranda trusts Billy who trusts Ariel who trusts Miranda, but there has not been enough interactions in the opposite direction to establish trust. When these three people meet, shall they trust each other? I.e., are they part of a circle of trust? The objective of this project is to develop an axiomatic theory to provide an answer to this question. In general, we start with a network were nodes represent individuals and directed edges represent a trust dissimilarity from the originating node to the end node. Small values of this dissimilarity signify large amounts of trust of the edge's source node on the edge's destination. Our goal is the study of the formation of trust groups in the network. I.e., the determination of the level of trust at which two individuals are integrated in a trust cluster given not only their direct interactions but their indirect interactions through other members of the network. It may make sense for Miranda, Billy, and Ariel to trust each other, because they all either trust each other directly, or have trust on someone that trusts the person they don't know. 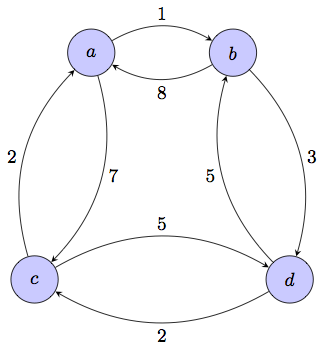 Figure 1. Trust network. Arcs denote trust dissimilarity, e.g., $a$ has substantial trusts in $b$, but $b$ has little trust in $a$. Clustering intuition is precarious. Nodes seem close clockwise but far apart counterclockwise. Once the problem is written in this language it is clear that determining circles of trust is akin to finding clusters in an asymmetric network for a given resolution level. The determination of a family of clusterings indexed by this resolution parameter is a problem known as hierarchical clustering. Simple as this sounds, the problem is that clustering in general and clustering using asymmetric data in particular is a poorly understood problem. There are plethora of methods that can be chosen to perform clustering, but these methods are based on heuristic intuition, not fundamental principles. Beyond purist concerns, lack of theoretical understanding is also a practical problem for clustering of asymmetric data because the intuition backing clustering methods is drawn from geometric point clouds. This intuition does not carry when the given data is not metric as in the case of asymmetric trust dissimilarities. E.g., in the network in Fig. 1 nodes $a$ and $b$ are closest to each other clockwise, but farthest apart counterclockwise, $c$ and $d$ seem to be closest on average, yet, it seems that all nodes are relatively close as it is possible to circle the graph clockwise without encountering a dissimilarity larger than 3. Even though asymmetric clustering intuition is difficult in general, there are some particular specks of intuition that we can exploit to gain insight into the general problem. These intuitive statements can be postulated as axioms that restrict the space of allowable asymmetric hierarchical clustering methods. To the extent that the axioms are true, the properties of this reduced space of methods are fundamental properties of asymmetric hierarchical clustering and by extension fundamental properties of the formation of circles of trust. This is the approach advocated in this project. Axioms of value and transformationIn our preliminary investigations we have postulated three axioms that we call the axioms of value, influence, and transformation. These axioms are stated formally in our published work but they correspond to the following intuitions: 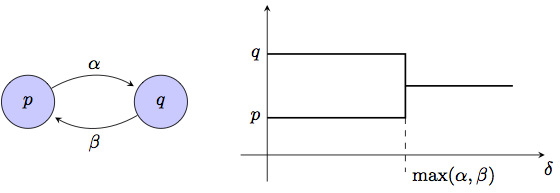 Figure 2. Axiom of Value. For a two node network nodes are clustered together at the resolution at which both can influence each other.
Axiom (A1) says that in a network with two nodes $p$ and $q$ and dissimilarities $A_X(p,q)=\alpha$ and $A_X(q,p)=\beta$, the nodes are reported as separate clusters for resolutions $\delta<\max(\alpha,\beta)$ and as a single cluster for resolutions $\delta\geq\max(\alpha,\beta)$. This is reasonable because at resolutions $\delta<\max(\alpha,\beta)$ one node can influence the other but not vice versa, which in most situations means that the nodes are not alike since trust flows in a single direction. Axiom (A2) states that increasing the level of trust between some nodes may result in the formation of additional circles of trust but cannot result in the dissolution of existing circles. This is erasable because a reduction in trust dissimilarities is expected to generate more trust in the network. 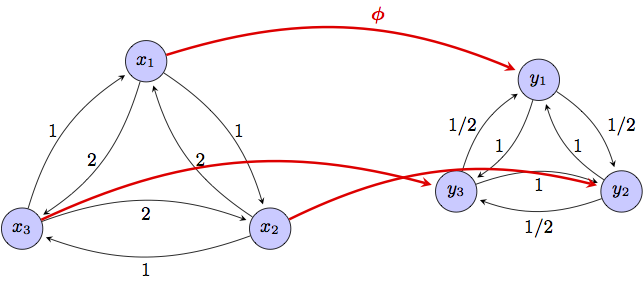 Figure 3. Axiom of Transformation. A dissimilarity reducing map $\phi:X\to Y$ produces dendrograms where clusters in the original network may be combined in the transformed network but cannot be separated. Despite their apparent weakness, axioms (A1)-(A2) are a source of strong structure. Our first preliminary result is the derivation of two asymmetric hierarchical clustering methods that abide to these axioms. The first method insists that trust propagate only through arcs in which there is bidirectional trust and is therefore termed reciprocal clustering. The second method allows trust to propagate unidirectionally and is thus termed nonreciprocal clustering. That these methods comply with (A1)-(A2) is not particularly surprising. However, we have proved that any clustering method that satisfies axioms (A1)-(A2) lies between reciprocal and nonreciprocal clustering in a well defined sense. Specifically, any clustering method that satisfies axioms (A1)-(A2) forms circles of trust at resolutions larger than the resolutions at which they are formed with nonreciprocal clustering, and smaller than the resolutions at which they are formed with reciprocal clustering. These preliminary result endows reciprocal and nonreciprocal clustering with special meaning. For a given resolution level, nodes that {\it do not} cluster together with nonreciprocal clustering cannot be part of a circle of trust. Nodes that {\it do} cluster together with reciprocal clustering are definitely part of a circle of trust. In between, the answer depends on the extent to which reciprocal trust propagation is required or nonreciprocal trust propagation is acceptable. Ongoing work
Acknowledgments and referencesThis is the Ph.D. work of Santiago Segarra. Also part of this project are Prof. Facundo Memoli and Prof. Gunnar Carlsson. This work builds on their prior work on hierarchical clustering for metric data and would not be possible without their contribution. Some preliminary results have appeared in the following paper:
|