VCDim
Generalization bounds for infinite classes: VC dimension
We will now consider the case where our hypothesis space is infinite, for example, hyperplanes of dimension {$m$}. As before, our learning algorithm selects a hypothesis h from {$\mathcal{H}$} based on a sample {$D$} of n i.i.d. examples {$\{\mathbf{x}_i,y_i\}$} from {$P(\mathbf{x},y)$}, which will denote as {$D\sim P^n$}. We will denote the {$0/1$} training data error (also called loss) of a hypothesis h as
{$L_D(h) = \frac{1}{n} \sum_i \mathbf{1}(h(\mathbf{x}_i)\ne y_i)$}
and we'll denote the true error as
{$L_P(h) = \mathbf{E}_{(\mathbf{x},y)\sim P} [\mathbf{1}(h(\mathbf{x})\ne y)]$}
For finite hypothesis spaces, we showed in the last lecture that:
Theorem: With probability {$1-\delta$} over the choice of training sample of size {$n$}, for all hypotheses {$h$} in {$\mathcal{H}$}:
{$L_P(h) - L_D(h) \le \sqrt{\frac{\log |\mathcal{H}| + \log\frac{1}{\delta}}{2n}}$}
We now consider the case of infinite hypothesis spaces, for example, hyperplanes. To bound the error of a classifier from a class {$\mathcal{H}$} using {$n$} examples, what matters is not the pure size of {$\mathcal{H}$}, but its richness: the ability to fit any dataset of size {$n$} perfectly. Perhaps the most fundamental measure of richness (or power or complexity or variance) of a hypothesis class studied in machine learning is called the Vapnik-Chervonenkis dimension (named for two Russian mathematicians, Vladimir Vapnik and Alexey Chervonenkis). For example, one can show that the VC-dimension of a class of hyperplanes of dimension {$m$} is {$m+1$}. In general, VC-dimension can be related to the number of parameters in a very complicated way. A fundamental result by Vapnik and Chervonenkis is that the {$\log |\mathcal{H}|$} in the bounds can be replaced by a function of the {$VC(\mathcal{H})$}:
Theorem: With probability {$1-\delta$} over the choice of training sample of size {$n$}, for all hypotheses in {$\mathcal{H}$}:
{$L_P(h) - L_D(h) \le \sqrt{\frac{VC(\mathcal{H})(\log\frac{2n}{VC(\mathcal{H})} + 1) + \log\frac{4}{\delta}}{n}}$}
We will not prove this theorem, as the proof is somewhat involved. In order to understand what it means, we need to define several terms.
VC-dimension of hyperplanes
Consider linear separators in 2 dimensions: {$sign(w_1 x_1 + w_2 x_2 + b)$}. For a set of three non-collinear points, there are {$2^3 =8$} possible labelings, and we can always find a hyperplane with zero error:
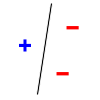 | 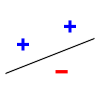 | 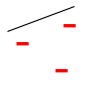 |
However, with 4 points, there are labelings no hyperplane in 2D can fit:
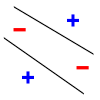
More generally, we define the notion of shattering.
Definition: A hypothesis class {$\mathcal{H}$} shatters a set of instances {$S = \{\mathbf{x}_1,\ldots,\mathbf{x}_n\}$} where {$\mathbf{x}_i \in \mathcal{X}$} if for every possible labeling {$\{y_1,\ldots,y_n\}$} with {$y_i\in\pm 1$}, there is an {$h\in\mathcal{H}$} with zero error: {$h(\mathbf{x}_i) = y_i, \;\; i=1,\ldots,n$}.
So hyperplanes in 2-D shatter any set of 3 non-collinear points, but there are sets of 4 points in 2-D that cannot be shattered by 2D hyperplanes. VC-dimension measures the size of the largest set that can be shattered by the class.
Definition: The VC-dimension of a class {$\mathcal{H}$} over the input space {$\mathcal{X}$} is the size of the largest finite set {$S \subset \mathcal{X}$} shattered by {$\mathcal{H}$}.
To show the VC-dimension of a class is v, we need to show:
- There exists a set {$S$} of size {$v$} shattered by {$\mathcal{H}$} (usually easy)
- There does not exists a set {$S$} of size {$v+1$} shattered by {$\mathcal{H}$} (usually harder)
Proof sketch of {$VC(\mathcal{H}) = 3$} for 2D hyperplanes {$\mathcal{H} = \{ h(\mathbf{x}) = sign(w_1 x_1 + w_2 x_2 + b)\}$}.
- The 3 pictures above with 3 points, plus an explanation that the other 5 cases are analogous is enough to show {$VC(\mathcal{H}) \ge 3$}.
- For 4 points: if any 3 points are collinear, then {$\mathcal{H}$} cannot shatter them, so we don't have to worry about shattering collinear sets of points. So pick any 3 points, which form a triangle, and then the fourth point is either inside the triangle or outside. If it's inside, label it with a plus and others with a minus and this cannot be fit with a line. If it's outside, draw lines from this point to the 3 others. If none of the lines intersect the triangle, then we're back to the first case, where one point is inside the hull of the other 3. If one of the lines intersects a side of the the triangle, then label the points linked by this line as plus and the others as minus and we're in the xor case: there is no way to separate pairs of points linked by intersecting segments with a line.
In general, we can show the VC dimension of hyperplanes in m dimensions is {$m+1$}. However, the number of parameters of a classifier is not necessarily it's VC dimension. Here are few other examples.
Classes with infinite VC dimension
- 1-Nearest Neighbor classifier in any dimension can shatter an infinite number of points.
- In 1 dimension, {$sign(sin(wx+b))$} has infinite VC-dimension.
