PAC
Generalization bounds for finite hypothesis classes
Consider the case where our hypothesis space is finite, for example, all decision trees of fixed depth. Our learning algorithm selects a hypothesis h from {$\mathcal{H}$} based on a sample {$D$} of n i.i.d. examples {$\{\mathbf{x}_i,y_i\}$} from {$P(\mathbf{x},y)$}, which will denote as {$D\sim P^n$}. We will denote the {$0/1$} training data error (also called loss) of a hypothesis h as:
{$L_D(h) = \frac{1}{n} \sum_i \mathbf{1}(h(\mathbf{x}_i)\ne y_i)$}
and we'll denote the true error as
{$L_P(h) = \mathbf{E}_{(\mathbf{x},y)\sim P} [\mathbf{1}(h(\mathbf{x})\ne y)]$}
The true error of the hypothesis we select based on low training error is most likely larger than the training error. Can we bound the difference in terms of the complexity of our hypothesis space {$\mathcal{H}$}?
A bound for zero training error learning
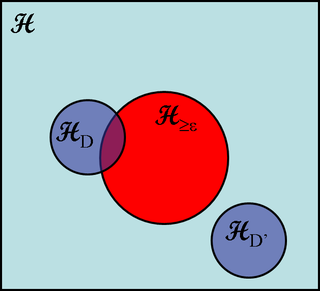
Suppose our algorithm finds a hypothesis consistent with the data, {$L_D(h)=0$}. We are interested in the probability (over all possible training samples D) that h could have {$L_P(h)\ge\epsilon$}. Let's denote the set of hypothesis consistent with D as {$\mathcal{H}_D \subseteq \mathcal{H}$} and the set of hypotheses that have true error greater than {$\epsilon$} as {$\mathcal{H}_{\ge\epsilon} \subseteq \mathcal{H}$}. Note that {$\mathcal{H}_D$} is a random subset of {$\mathcal{H}$}, while {$\mathcal{H}_{\ge\epsilon}$} is fixed. The problem for the learner occurs when the two overlap, since in the worst case, a consistent hypothesis can end up being from {$\mathcal{H}_{\ge\epsilon}$}.
We're going to bound the probability that the overlap is non-empty. Consider a given hypothesis h that has true error greater than {$\epsilon$}, {$h\in \mathcal{H}_{\ge\epsilon}$}. The probability that it has made zero errors on {$D$}, {$h \in \mathcal{H}_D$}, is exponentially small in {$n$}:
{$Pr_{D\sim P^n}(L_D(h)=0) \le (1-\epsilon)^n$}
Now suppose that there are K hypotheses with true error greater than {$\epsilon$}, i.e. {$\mathcal{H}_{\ge\epsilon} = \{h_1,\ldots,h_K\}$}. What is the probability that any of them is consistent with the data D?
{$Pr_{D\sim P^n}(\exists h \in \mathcal{H}_{\ge\epsilon}: h\in\mathcal{H}_D) = Pr_{D\sim P^n}(h_1 \in \mathcal{H}_D\vee \ldots \vee h_K \in \mathcal{H}_D)$}
where {$\vee$} is the logical or symbol. To bound the probability of a union of events, we use the the union bound:
{$\textbf{Union Bound:}\;\;\; P(A \cup B) \le P(A) + P(B)$}
Hence
{$Pr_{D\sim P^n}(\exists h \in \mathcal{H}_{\ge\epsilon}: h \in \mathcal{H}_D ) \le K (1-\epsilon)^n$}
To make this bound useful, we will simplify it at the expense of further looseness. Since we don't know K in general, we will upper-bound it by {$|\mathcal{H}|$} and since {$(1-\epsilon) \le e^{-\epsilon}$} for {$\epsilon \in [0,1]$}, we will write:
{$Pr_{D\sim P^n}(\exists h \in \mathcal{H}_{\ge\epsilon}: h \in \mathcal{H}_D) \le |\mathcal{H}| e^{-n\epsilon}$}
Hence the probability that our algorithm will select a hypothesis with true error greater than {$\epsilon$} given that it selected a hypothesis with zero training error is bounded by {$|\mathcal{H}| e^{-n\epsilon}$}, which decreases exponentially with {$n$}.
What's a bound good for?
There are two ways to use the bound. One is to set the probability of failure, {$\delta$} and the number of examples {$n$} and ask about the smallest {$\epsilon$} for which the bound holds.
{$\delta = |\mathcal{H}| e^{-n\epsilon} \rightarrow \epsilon = \frac{\log |\mathcal{H}| + \log \frac{1}{\delta}}{n}$}
So with prob. {$1 - \delta$} over the choice of training sample of size n, for any hypothesis h with zero training error,
{$L_P(h) \le \frac{\log |\mathcal{H}| + \log \frac{1}{\delta}}{n}$}
The other way to use it is to fix {$\delta$} and {$\epsilon$} and ask how many examples are need to guarantee them (sample complexity). That is:
{$\delta = |\mathcal{H}| e^{-n\epsilon} \rightarrow n = \frac{1}{\epsilon}(\log |\mathcal{H}| + \log \frac{1}{\delta})$}
The PAC (Probably Approximately Correct) framework asks these questions about different hypothesis classes and considers a class PAC-learnable if the number of examples needed to learn a probably (with prob. {$\delta$}), approximately (true error of at most {$\epsilon$}) correct hypothesis is polynomial in parameters of the class (e.g. depth of the tree, dimension of hyperplane, etc.) as well as in {$\epsilon$} and {$\frac{1}{\delta}$} (or {$\log\frac{1}{\delta}$}).
This is the simplest of generalization bounds but their form remains the same: the difference in the true error and training error is bounded in terms of complexity of the hypothesis space. The limitation of the above bound is that it considers finite classes (we will deal with this when we get to VC dimension), but even for finite classes, we have only considered hypotheses with zero training error, which may not exist.
A bound for non-zero training error learning
We will need a form of Chernoff bound for biased coins: suppose we have {$n$} i.i.d. examples {$ z_i \in \{0,1\} $} where {$P(z_i = 1) = p$}. Let {$\overline{z} = \frac{1}{n} \sum_i z_i$} be the proportion of 1s in the sample. Then {$Pr(p - \overline{z} \ge \epsilon) \le e^{-2n\epsilon^2}$}
Given a hypothesis {$h$}, the probability that the difference between its true error and training error is greater than {$\epsilon$} is bounded:
{$Pr_{D\sim P^n}(L_P(h) - L_D(h) \ge \epsilon) \le e^{-2n\epsilon^2}$}
Now we need to bound the probability of observing the difference for all hypotheses, so that we can pick the one with lowest error safely. Again, we use the union bound:
{$Pr_{D\sim P^n}(\exists h \in \mathcal{H} : L_P(h) - L_D(h) \ge \epsilon) \le |\mathcal{H}| e^{-2n\epsilon^2}$}
Setting {$\delta = |\mathcal{H}| e^{-2n\epsilon^2}$} and solving, we get: with prob. {$1-\delta$} over the choice of training sample of size {$n$}, for all hypotheses in {$\mathcal{H}$}:
{$L_P(h) - L_D(h) \le \sqrt{\frac{\log |\mathcal{H}| + \log\frac{1}{\delta}}{2n}}$}
In case of non-zero training error, the number of samples needed decreases with the square root of 1/n, as opposed to with 1/n, which is much slower.
Consider the sizes of some simple hypotheses spaces. The class {$\mathcal{H}$} of all Boolean functions on m binary attributes {$|\mathcal{H}| = 2^{2^m}$}, since we can choose any output for any of the {$2^m$} possible inputs.
Clearly, this class is too rich, since {$\log_2 |\mathcal{H}| = 2^m$}. The class of decision trees of depth {$k$} on {$m$} binary attributes is of size {$O((2m)^{2^k-1})$}, which is really large if {$k$} is not fixed and will require a large number of samples to learn accurately.
On can also show that these bounds can be essentially tight, i.e. there are pathological examples where we need that many samples. What these bounds tell us is to learn from a small number of examples, we need a small hypothesis space. We will consider finer-grained notions of complexity when we look at VC-dimension. Back to Lectures