Clustering
Clustering
In unsupervised learning, our data consists only of inputs {$\mathbf{x}_1,\ldots,\mathbf{x}_n$}. The goal of unsupervised learning is to discover the structure of the data, and one of the primary types of structure is a partition of the data into coherent clusters. Data often has many kinds of structure, so there are many possible ways to group examples by similarity to each other.
K-Means Algorithm
K-Means is a very simple, iterative clustering algorithm:
- Init: pick K cluster centroids at random (for a better way to init, see: kmeans++)
- Alternate until convergence:
- Assign examples to nearest centroid
- Set centroid to be the mean of the examples assigned to it
Here is an example run in toy 2-D data, using this applet: http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/AppletKM.html.
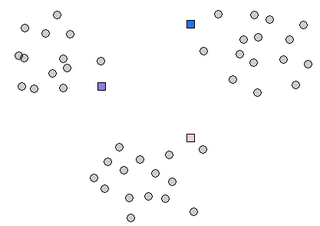
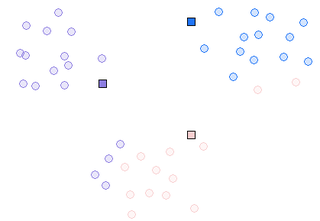
Initialization step of the algorithm is very important and can greatly effect the outcome. Here's an example where bad initialization leads to bad clusters.
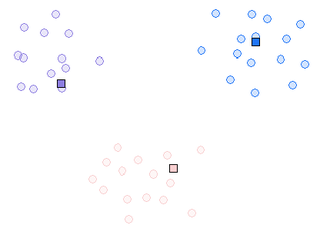
A better initialization leads to different clusters:
Here's an example of applying K-means to pixels of an image from http://www.cs.washington.edu/research/imagedatabase/demo/kmcluster/
K-means is a workhorse of many data intensive applications, where it's often used to quantize or compress the data. In speech recognition and computer vision, high-dimensional signals are commonly quantized into discrete clusters and then used in more complex models or as features for classification.
K-means objective
K-means can be interpreted as a greedy algorithm: but what objective function is it optimizing? Let's define {$\mu_1,\ldots,\mu_K$} as the centroids of the clusters (note that each {$\mu_k$} is a vector of the same dimension as {$\mathbf{x}$}) and {$r_{ik}$} as binary variables indicating whether datapoint {$\mathbf{x}_i$} belongs to cluster {$k$}. The K-means objective is the so-called distortion, the sum of distances of centroids to their cluster members:
{$J(\mu,r) = \sum_{i=1}^n\sum_{k=1}^K r_{ik} ||\mu_k-\mathbf{x}_i||^2_2$}
K-means alternatively changes the {$\mu$}s and the {$r$}s in order to greedily optimize {$J(\mu,r)$}. Fixing the centroids, for each point {$i$}, we assign it to the closest centroid:
{$\arg \min_r J(\mu,r) \rightarrow r_{ik} = \textbf{1}(k = \arg \min_{k'} ||\mu_{k'} - \mathbf{x}_i||_2^2) $}
Fixing the cluster membership variables, the centroids are set to be the means:
{$\arg \min_\mu J(\mu,r) \rightarrow \mu_k = \frac{\sum_i r_{ik} \mathbf{x}_i}{\sum_i r_{ik}}$}
This objective function is NP-hard to optimize in dimension d even for 2 clusters and also NP-hard in 2D for arbitrary number of clusters k. In practice, the greedy algorithm above is typically run many times from different random init starts and works pretty well when the dimensions is not too high (around 10-20) and k is not too large (5-10). There several tricks that can help it, like PCA-ing the data first down to a smaller dimension.
Kernelized K-means
Like many algorithms we have seen that use Euclidean distances and dot products, K-means can also be kernelized. Suppose we have a kernel {$k(\mathbf{x},\mathbf{x}') = \phi(\mathbf{x})^\top\phi(\mathbf{x}')$}. Then the two steps of the algorithm are:
{$\arg \min_r J(\mu,r) \rightarrow r_{ik} = \textbf{1}(k = \arg \min_{k'} ||\mu_{k'} - \phi(\mathbf{x}_i)||_2^2) $}
Fixing the cluster membership variables, the centroids are set to be the means:
{$\arg \min_\mu J(\mu,r) \rightarrow \mu_k = \frac{\sum_i r_{ik} \phi(\mathbf{x}_i)}{\sum_i r_{ik}}$}
We can express {$||\mu_{k} - \phi(\mathbf{x})||_2^2$} purely in terms of the kernel function. Define {$n_k = \sum_i r_{ik}$}. Then
{$ ||\mu_k - \phi(\mathbf{x})||^2_2 = \mu_k^\top\mu_k - 2\mu_k^\top\phi(\mathbf{x}) +\phi(\mathbf{x})^\top\phi(\mathbf{x}) = \frac{1}{n_k^2}\sum_{i,j} r_{ik}r_{jk}k(\mathbf{x}_i,\mathbf{x}_j) - \frac{2}{n_k}\sum_i r_{ik} k(\mathbf{x}_i,\mathbf{x})+ k(\mathbf{x},\mathbf{x}) $}
Using this kernel expansion, we can run the algorithm without ever explicitly storing {$\mu$}.