Regression
Continuous variable prediction
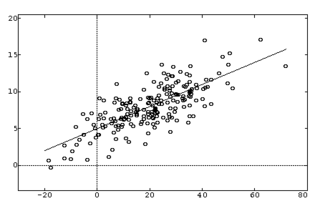
Suppose now instead of just measuring a single variable of interest, like the amount of coffee in your cup you buy each morning at your coffeeshop, we have some other possibly relevant measurements that can help us predict it. For example, how busy the place is, how good is the mood of the barista, the price of gas. As many smart people reportedly have said, "Prediction is hard, especially about the future." But we're going to try anyway, in the simplest way possible, using linear regression.
Linear regression
Consider first the case of a single variable of interest y and a single predictor variable x. The predictor variables are called by many names: covariates, inputs, features; the predicted variable is often called response, output, outcome.
We have some data {$D = \{x_i,y_i\}$} and we assume a simple linear model of this data with Gaussian noise:
{$Y = aX + b + Z \;\;\; {\rm with} \;\;\; Z \sim \mathcal{N}(0,\sigma^2)$}
Now, {$Y_i \sim \mathcal{N}(aX_i + b,\sigma^2)$}, so let's do MLE for a and b.
{$ \log P(D|a,b) = -n\log (\sigma\sqrt{2\pi}) - \sum_i \frac{(y_i - ax_i - b)^2}{2\sigma^2}$}
Note that the negative log-likelihood is simply residual squared error {$\frac{1}{2}\sum_i (y_i - ax_i - b)^2$} (divided by {$\sigma^2$}). Setting derivatives wrt to a and b to 0, we get linear equations (called normal equations) in a,b:
{$ \; \begin{align*}\sum_{i} \frac{x_{i}(y_{i} - ax_{i} - b)}{\sigma^{2}} & = 0 \rightarrow a\sum_{i} x^2_{i} + b \sum_{i} x_{i} & = \sum_{i} y_{i} x_{i} \\ \sum_{i} \frac{y_{i} - ax_{i} - b}{\sigma^{2}} & = 0 \rightarrow a\sum_{i} x_{i} + b n & = \sum_{i} y_{i} \end{align*} \; $}
For this problem, we can solve for a and b by hand (please do, it's a good exercise), but in general we will have many predictors (inputs).
Multivariate case
Now our features are vectors of dimension m which we will denote in boldface as {$\textbf{x}_i$} and we will index the j-th feature of i-th example as {$x_{ij}$}. So we will arrange all the examples in a matrix {$\textbf{X}$}, with rows {$\textbf{x}_i$}, as follows:
{$\left( \begin{array}{ccc} x_{11} & \ldots & x_{1m} \\ \vdots & \vdots & \vdots \\ x_{n1} & \ldots & x_{nm} \end{array} \right) $}
Similarly, we arrange all the outcomes in a column vector {$\textbf{y}$} of height n. We assume a linear model with m coefficients, which we arrange in a column vector {$\textbf{w}$}:
{$ y_i = \sum_j w_j x_{ij} + \mathcal{N}(0,\sigma^2) = \textbf{x}_{i}\textbf{w} + \mathcal{N}(0,\sigma^2) $}
As above, maximizing log likelihood is equivalent (up to a scaling and additive term) to minimizing residual squared error:
{$ \; \begin{align*} \log P(D \mid \textbf{w},\sigma) & = -n\log(\sigma\sqrt{2\pi}) - \frac{1}{2\sigma^2}\sum_i (y_i - \textbf{x}_{i}\textbf{w})^2 \\ & = -n\log(\sigma\sqrt{2\pi}) - \frac{1}{2\sigma^2}(\textbf{y} - \textbf{X}\textbf{w})^\top(\textbf{y}-\textbf{X}\textbf{w}) \end{align*} \; $}
Before computing the MLE, let's define the vector {$\textbf{r} = (\textbf{y}-\textbf{X}\textbf{w})$}, as the residual or error vector. The layout of all these vectors and matrices together is:
{$ \left( \begin{array}{c} r_{1} \\ \vdots \\ r_{n} \end{array} \right) = \left( \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right) - \left( \begin{array}{ccc} x_{11} & \ldots & x_{1m} \\ \vdots & \vdots & \vdots \\ x_{n1} & \ldots & x_{nm} \end{array} \right) \left( \begin{array}{c} w_{1} \\ \vdots \\ w_{m} \end{array} \right) $}
What happened to the constant term?
In the single feature case, we included b, the constant term. We dropped it for the multivariate case. Fortunately, it's easy to add it back by simply including an extra feature that is always 1.
What about polynomial or non-linear regression?
Suppose that dependence on some original feature (barista's mood, gas price) is not linear, but quadratic or cubic or sinusoidal or other non-linear function, {$f(x)$}. Simple: we just add {$f(x)$} as a new feature.
MLE
Taking (vector) derivatives of the residual squared error with respect to the parameters, we get: (if you need a refresher and a good quick reference on matrix manipulations, the Matrix Cookbook is very handy)
{$ \frac{\partial}{\partial \textbf{w}} \frac{\textbf{r}^\top\textbf{r}}{2} = -\textbf{X}^\top(\textbf{y}-\textbf{X}\textbf{w}) = 0 \;\;\; \rightarrow \;\;\ \textbf{w}_{MLE} = (\textbf{X}^\top\textbf{X})^{-1} \textbf{X}^\top\textbf{y} $}
Of course, we need {$\textbf{X}^\top\textbf{X}$} to be invertible. When is that a problem? When the features are not linearly independent.
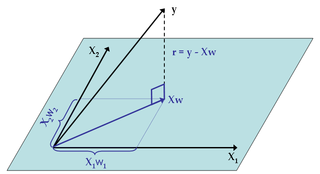
The regression coefficients we derived from MLE are often called Ordinary Least Squares (OLS). There are many other variants, and we'll see some soon. If you're wondering what the MLE/OLS is doing geometrically, there is a nice interpretation: If we view the outcomes {$\textbf{y}$} as a vector in Euclidean space, and similarly view each input variable (i.e. each column of the data matrix {$\textbf{X}$}) as a vector the same space, then the least squares regression is equivalent to an orthogonal projection of {$\textbf{y}$} onto the subspace spanned by the input variables (or equivalently, to the column space of X). The projected vector is the prediction {$\textbf{X}\textbf{w}_{MLE}=\textbf{P}\textbf{y}$} where {$\textbf{P} = \textbf{X}(\textbf{X}^\top\textbf{X})^{-1}\textbf{X}^\top$} is the projection matrix, in this case called the 'hat' matrix, which maps from {$\textbf{y}$} to {$\hat{\textbf{y}}$}, since {$\hat{\textbf{y}} = \textbf{ X w} = \textbf{X}(\textbf{X}^\top\textbf{X})^{-1}\textbf{X}^\top \textbf{y}$}. This relationship is depicted for three examples and two input variables (in the picture {$\textbf{w}$} refers to {$\textbf{w}_{MLE}$}):
MAP
And now for the Bayesian way, of course. We will assume a prior on the parameters we are trying to estimate, in this case, {$\textbf{w}$}. We will pick the simplest and most convenient one, the Gaussian. Since we usually don't really know much a priori about {$\textbf{w}$}, we will use a prior mean of 0 and a standard deviation {$\gamma$} for each parameter:
{$ w_j \sim \mathcal{N}(0,\gamma^2)\;\; {\rm so}\;\; P(\textbf{w}) = \prod_j \frac{1}{\gamma\sqrt{2\pi}} e^{\frac{-w_j^2}{2\gamma^2}} $}
Where do we get {$\gamma$}? We use cross-validation. So now to get MAP we need:
{$ \begin{align*}\arg\max_\textbf{w} \log P(\textbf{w} \mid D, \sigma,\gamma) & = \arg\max_\textbf{w} \left(\log P(D \mid \textbf{w}, \sigma) + \log P(\textbf{w} \mid \gamma)\right) \\ & = \arg\min_\textbf{w} \left( \frac{1}{2\sigma^2} \textbf{r}^\top\textbf{r} + \frac{1}{2\gamma^2} \textbf{w}^\top\textbf{w} \right) \end{align*} $}
Note the effect of the prior: it penalizes large values of {$\textbf{w}$}.
Taking derivatives, we get:
{$ \frac{\partial}{\partial \textbf{w}} \left(\frac{\textbf{r}^\top\textbf{r}}{2\sigma^2} + \frac{\textbf{w}^\top\textbf{w}}{2\gamma^2}\right) = -\frac{1}{\sigma^2}\textbf{X}^\top(\textbf{y}-\textbf{X}\textbf{w})+ \frac{1}{\gamma^2}\textbf{w} = 0 $}
which leads to:
{$ \textbf{w}_{MAP} = (\textbf{X}^\top\textbf{X} + \frac{\sigma^2}{\gamma^2} \textbf{I})^{-1} \textbf{X}^\top\textbf{y} $}
There are several trends to observe. As {$\gamma \rightarrow \infty$}, which means our prior is getting broader, MAP reduces to MLE. As the number of samples increases while {$\gamma$} and {$\sigma$} stay fixed, the effect of the prior vanishes, since the entries of {$\textbf{X}^\top\textbf{X}$} grow linearly with n. As the noise parameter {$\sigma$} decreases, the effect of the prior also vanishes. As the noise parameter {$\sigma$} increases, MAP shrinks towards prior mean of 0, {$\textbf{w}_{MAP} \rightarrow 0$}.
The MAP regression above (assuming a zero-mean Gaussian prior) is often called Ridge Regression, where ridge refers to the quadratic penalty of the weights. There are many other priors you can assume, of course, and we'll also see some soon.