PointEstimation
Point Estimation Basics: Biased Coin
Before we get to any complex learning algorithms, let's begin with the most basic learning problem.
Suppose you found a funny looking coin on your way to class and, being a scientist, started flipping it.
What is the simplest model of this scientific experiment? Each flip is a Bernoulli (binary) variable, independently and identically distributed (i.i.d.):
{$P(H) = \theta \; {\rm and} \;P(T) = 1-\theta, \; {\rm where}\; \theta \in [0,1].$}
So if you flip the coin {$n$} times, with {$n_H$} heads and {$n_T$} tails, the likelihood of observing a sequence (data) D is:
{$ P(D\mid\theta) = \theta^{n_H}(1-\theta)^{n_T}$}.
Maximum Likelihood Estimation (MLE) for the coin
Suppose you observe 3 heads and 2 tails. What's your guess for {$\theta$}? If you guessed 3/5, you might be doing MLE, which is simply finding a model that best explains your experiment:
{$ \hat\theta_{MLE} = \arg \max_\theta P(D\mid\theta)$}
How do we find the {$\theta$} that maximizes the log-likelihood of the data? Let's try to take the derivative and set it equal to zero. Before we do that though, let's change the product of {$\theta$}-dependent terms to a sum of terms --- this will make it slightly easier to deal with the derivative. We can get a sum from our product by simply taking the log:
{$\log P(D\mid\theta) = n_H\log(\theta) + n_T\log(1-\theta)$}
Notice that since log is a an increasing monotonic function, taking the log doesn't change the {$\arg \max$}:
{$\arg \max_\theta P(D\mid\theta) = \arg \max_\theta \; \log P(D\mid\theta)$}
so taking log in this case doesn't change the overall answer we'll get for {$\theta$}. Now, let's take the derivative and set it equal to zero:
{$ \; \begin{align*} \frac{d}{d\theta} \log P(D\mid\theta) & = 0 \\ \frac{n_H}{\theta} - \frac{n_T}{1 - \theta} & = 0 \\ n_H(1 - \theta) & = n_T\theta \\ \hat\theta_{MLE} & = \frac{n_H}{n_H+n_T}. \end{align*} \; $}
Why and when is it a good idea to set the parameters of a model by MLE? In practice, the MLE principle is a basis for a majority of practical parameter estimation algorithms, as we will see. If you have enough data and the correct model, MLE is all you need: it will find the true parameters.
The problem is that you rarely have either enough data or the perfect model, so MLE can be terribly wrong. Example: suppose all five tosses come up heads, would you believe MLE? What about five million tosses, all heads?
As another example, consider deriving MLE for the multinomial distribution for estimating a model of a die (ours is a different definition than wikipedia). Suppose there are {$K$} sides of the die (let's call them labels or outcomes), so the model is
{$P(X = j) = \theta_j \;\; 1 \le j \le K-1, \; \; P(X = K) = 1 - \sum_{j=1}^{K-1} \theta_j $}
(We can also define {$\theta_K$} and introduce a sum to 1 constraint on the parameters -- then we would have to use the method of Lagrange multipliers -- we'll do it that way later in the course using the EM algorithm, see the M-step...)
We are given a dataset D of {$n$} samples, of which {$n_j$} have label/outcome {$j$} and {$n = \sum_{j=1}^K n_j$}. The log likelihood is {$\log P(D|\theta) = \sum_{j=1}^{K-1} n_j \log \theta_j + n_K \log (1 - \sum_{k=1}^{K-1} \theta_k ) $}
Taking partial derivates for each parameter, we have:
{$ \begin{align*} \frac{\partial}{\partial\theta_j} \log P(D\mid\theta) & = 0, \;\;\; 1 \le j \le K-1 \\ \frac{n_j}{\theta_j} - \frac{n_K}{1 - \sum_{k=1}^{K-1}\theta_k} & = 0, \;\;\; 1 \le j \le K-1\\ \frac{1-\sum_{k=1}^{K-1} \theta_k }{n_K} &= \frac{\theta_j}{n_j}, \;\;\; 1 \le j \le K-1 . \end{align*} $}
Since the last equation holds for every j and the left hand side does not depend on j, we have that for some constant C, {$ \theta_j = C n_j, \;\; 1 \le j \le K-1,\;\; {\rm and} \;\; 1-\sum_{k=1}^{K-1} \theta_k = C n_K $}. Plugging in {$ \theta_j = C n_j $} into the last equation, we have: {$ 1-\sum_{k=1}^{K-1} C n_k = C n_K $}. So C is 1/n. Hence the MLE is {$ \theta_j =\frac{n_j}{n} , \;\; 1 \le j \le K-1 $}.
One can also do cool math to get learning guarantees that tell you how accurate the estimates are as a function of how many observations you have.
The Bayesian way
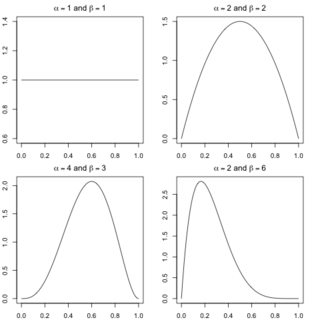
The fact is, that you have some experience with coins, so when you don't have enough data, you rely on your prior knowledge that most coins are pretty fair to estimate the parameter. If you're a Bayesian, you will embrace uncertainty but quantify it, by assuming that your prior belief about coin fairness can be described with a distribution {$P(\theta)$}. In particular, the Beta distribution, with several examples shown below, is a very convenient class of priors:
We'll talk about the exact form of the prior in a moment, but first, what do we do with it? The Bayesian framework uses data to update this prior distribution over the parameters. Using Bayes rule, we obtain a posterior over parameters:
{$ P(\theta | D) = \frac{P(D | \theta) P(\theta)}{P(D)} \propto P(D | \theta) P(\theta) $}
Now let's look at the Beta distribution:
{$ Beta(\alpha,\beta):\;\; P(\theta \mid \alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}$}
where {$\Gamma$} is the gamma function (for positive integers n, {$\Gamma(n)=(n-1)!$}). The hyperparameters {$\alpha\ge 1,\beta \ge 1 $} control the shape of the prior: their sum controls peakiness and their ratio controls the left-right bias. Why is Beta so convenient? Here's why:
{$ P(\theta | D) \propto P(D | \theta) P(\theta) \propto \theta^{n_H+\alpha-1}(1-\theta)^{n_T+\beta-1}$}
Hence, {$ P(\theta | D) = Beta(n_H+\alpha;n_T+\beta)$}. This property of fit between a model and its prior is called conjugacy, which essentially means the posterior is of the same distributional family as the prior.
OK, so now we have a posterior, but what if we want a single number (an estimate). The most common answer, basically because it is often computationally the easiest, is the maximum a posteriori (MAP) estimate:
{$ \hat\theta_{MAP} = \arg \max_\theta P(\theta\mid D) = \arg \max_\theta \left( \log P(D\mid\theta) + \log P(\theta) \right)$}
For the {$ Beta(\alpha;\beta)$} prior, the MAP estimate is:
{$ \hat\theta_{MAP} = \frac{n_H+\alpha-1}{n_H+n_T+\alpha+\beta-2} $}
Note that as {$ n = n_H+n_T \rightarrow \infty$}, the prior's effect vanishes and we recover MLE, which is what we want: in the evidence of enough data, prior shouldn't matter. We will see this vanishing prior effect in many scenarios.
MAP estimate is only the simplest Bayesian approach to parameter estimation. It sets our model parameter to the mode of the posterior distribution {$ P(\theta\mid D) $}. There is much more information in the posterior than is expressed by the mode; for instance, the posterior mean and variance of the parameter.
Why the mean? Suppose you want to predict what the probability is of the next flip coming up heads, given that the seen data is exactly the posterior mean:
{$ \; \begin{align*} P(X_{n+1} = H \mid D) & = \int_\theta P(X_{n+1}= H,\theta\mid D)d\theta \\ & = \int_\theta P(X_{n+1} = H \mid \theta)P(\theta\mid D)d\theta \\ & = \int_\theta \theta P(\theta\mid D)d\theta \end{align*} \; $}
In English: The probability that the next flip gives heads, given the previous outcomes D = The probability that the next flip gives heads, and that {$\theta$} is some value, summed (integrated) over all possible values of {$\theta$}. We then break up {$P(H,\theta|D) = P(H|\theta,D)P(\theta|D)= P(H|\theta)P(\theta|D)$}, (noting that once you know {$\theta$}, then {$D$} doesn't tell you anything more about the probability of heads and finally, note that {$P(H|\theta)$} is just {$\theta$}, since {$\theta$} is the probability of seeing heads.