LocallyWeightedRegression
Locally Weighted Regression
Our final method combines advantages of parametric methods with non-parametric. The idea is to fit a regression model locally, weighting examples by the kernel K.
Locally Weighted Regression Algorithm
- Given training data {$D=\{\mathbf{x}_i,y_i\}$}, Kernel function {$K(\cdot,\cdot)$} and input {$\mathbf{x}$}
- Fit weighted regression {$\hat{\mathbf{w}}(\mathbf{x}) = \arg\min_w \sum_{i=1}^{n} K(\mathbf{x}, \mathbf{x}_i) (\mathbf{w}^\top \mathbf{x}_i - y_{i})^2$}
- Return regression prediction {$\hat{\mathbf{w}}(\mathbf{x})^\top \mathbf{x}$}.
Note that we can do the same for classification, fitting a locally weighted logistic regression:
Locally Weighted Logistic Regression Algorithm
- Given training data {$D=\{\mathbf{x}_i,y_i\}$}, Kernel function {$K(\cdot,\cdot)$} and input {$\mathbf{x}$}
- Fit weighted logistic regression {$\hat{\mathbf{w}}(\mathbf{x}) = \arg\min_w \sum_{i=1}^{n} K(\mathbf{x}, \mathbf{x}_i) \log(1+\exp\{-y_i\mathbf{w}^\top \mathbf{x}_i\})$}
- Return logistic regression prediction {$sign(\hat{\mathbf{w}}(\mathbf{x})^\top \mathbf{x})$}.
The difference between regular linear regression and locally weighted linear regression can be visualized as follows:
 |  |
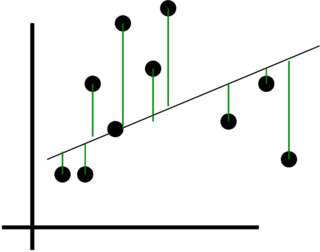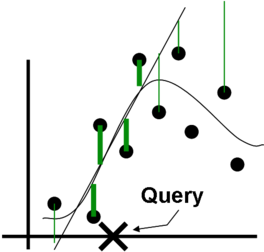Linear regression uses the same parameters for all queries and all errors affect the learned linear prediction. Locally weighted regression learns a linear prediction that is only good locally, since far away errors do not weigh much in comparison to local ones.
Here's a result of using good kernel width on our regression examples (1/32, 1/32 and 1/16 of x-axis width, respectively):
 |  |  |
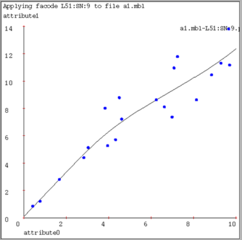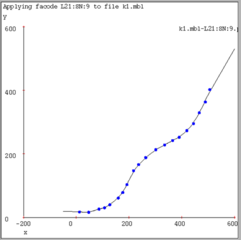