ProbabilityReview
Introductory Example
There are many techniques in machine learning that rely on estimating how likely the occurrence of an event is. For instance, we often want to be able to determine predictive relationships; perhaps when event {$A$} occurs, {$B$} generally follows. Or, we might have a complicated model of a million possible events, and wish to simplify the model by allowing it to neglect the least likely events. Both of these scenarios rely on the fields of probability and statistics.
To start out with, we need to define some terms, which is simpler to do with an example. So, imagine you have an oddly shaped stone, like so:
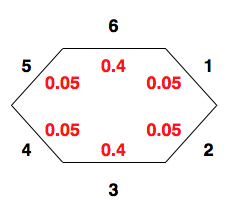
A strangely shaped stone, used as a die.
The black numbers are the values of the 6 sides of the stone, and the red numbers denote the probability that the stone will land with a particular side facing upwards on any given toss, where a toss is the "experiment" we're interested in. In probability, the term sample space is used to mean the set of all possible outcomes of an experiment, and is usually denoted by {$\Omega$}. In this example:
{$\Omega = \{1\; \textrm{is rolled}, 2\; \textrm{is rolled}, 3\; \textrm{is rolled}, 4\; \textrm{is rolled}, 5\; \textrm{is rolled}, 6\; \textrm{is rolled}\}$}
Notice also that the sum of all the red numbers equals 1. In probability, the number 1 corresponds to certainty, and the number 0 corresponds to impossibility. Since when we toss the die we are certain that some side will be facing up, it should make sense that the sum of the probabilities of all sides is 1.
Because the stone has no memory (it doesn't record past tosses), each toss we make is independent of all other tosses. Even if we've tossed the stone five times and gotten a 6 every time, this doesn't mean we're any more likely to get one of the other numbers on the next toss; probability of a 6 is still identical to what it was originally --- 0.4. If we toss the stone many times, recording how often each number comes up, our record will be distributed over the six possible events. These facts together form a term we'll see frequently in this class: independent and identically distributed (often abbreviated i.i.d). For many problems we'll encounter later in the semester, we'll make the assumption that data is i.i.d.; this is because if we have data that is NOT i.i.d., the computational complexity rises sharply, becoming intractable for all but the smallest of cases.
When we consider tossing the stone, we might also be interested in something more complex than just the probability of any single side. For instance, we might want to know how likely it is that a toss results in any even number. In this case, the "event" we're interested in is a toss that results in 2, 4, or 6. In general, the term event is used in probability to refer to any set of zero or more outcomes. Any event you can define, you should be able to combine the probabilities of the most basic events to determine the chance of your more complex event. This is what we'll assemble some tools for accomplishing in the rest of this recitation.
Combining Events
Using the probabilities of the stone described above, what is the probability that either a 1 or 6 come up on any particular toss? The answer is fairly clearly 0.45. But why is it so clearly 0.45? The answer is that each event is disjoint from the others; we can have either a 1 or a 6, but not both. This is an important requirement when combining events. If we don't take into account the fact the events may overlap, we might have a greater than 1 probability. So let's look at an example where the events do overlap. What is the probability that the stone's value on the next toss will be odd or a prime number? The probability that it will be odd is:
{$p(1) + p(3) + p(5) = 0.05 + 0.4 + 0.05 = 0.5,$}
and the probability that it will be prime is:
{$p(2) + p(3) + p(5) = 0.05 + 0.4 + 0.05 = 0.5.$}
If we try adding these two results together, we get {$0.5 + 0.5 = 1$}. But it can't be the case that probability of being odd or prime is 1, since the stone has some chance of landing with the 6 side facing up. The issue here is that we counted {$p(3)$} and {$p(5)$} twice in our sum. We need to make sure that we don't count the same outcome twice. And so we have the following rule:
{$p(A \cup B) = p(A) + p(B) - p(A \cap B)$}
In our example, {$A$} is the event that a toss will turn up an odd number, and {$B$} is the event that a toss will turn up a prime number. Since both {$A$} and {$B$} count the number 3, we remove one of the copies via {$P(A \cap B)$}. The equation above is one example of the Inclusion-Exclusion Principle.
Random Variables
Random variables are rather poorly named; they are not really random, nor are they really variables. Rather, they are more like functions that assign a unique number to each possible outcome of an experiment. In the case of the die above, the mapping is so straightforward as to be trivial. If we use X to denote our random variable in this case, then:
{$
X =
\begin{cases}
1,\; \textrm{if 1 faces up after the toss}
2,\; \textrm{if 2 faces up after the toss}
3,\; \textrm{if 3 faces up after the toss}
4,\; \textrm{if 4 faces up after the toss}
5,\; \textrm{if 5 faces up after the toss}
6,\; \textrm{if 6 faces up after the toss}
\end{cases}
$}
So, X just maps "if x faces up after the toss" to the number x. That is, {$X: \Omega \rightarrow \{1, 2, 3, 4, 5, 6\}$}. In the case of other experiments, the mapping can be less trivial. For instance, what if instead we had a coin and the experiment under consideration was a flip of this coin? Then the outcome space would be the set {$\{\textrm{heads}, \textrm{tails}\}$}. One possible way to map these outcomes to numbers would be:
{$
X =
\begin{cases}
1,\; \textrm{if heads}
; 2,\ \textrm{if tails}
\end{cases}
$}
Or, consider what the outcome space would be if we instead said that every "experiment" consists of 2 coin flips. Then our random variable would need to be a function from HH, TT, HT, TH to unique numbers, say 1, 2, 3, 4.
All these random variables are discrete, meaning outcomes can be mapped to the integers; the number of outcomes is countable. Naturally, there are also continuous random variables. For example, if the experiment under consideration was the temperature in Wu & Chen auditorium at 9:30 am, then the sample space would be {$(-\infty\,^{\circ}{\rm C}, \infty\,^{\circ}{\rm C})$}, and the random variable would again basically be the identity mapping here, to {$(-\infty, \infty)$}. Note that for continuous random variables we can have more concrete bounds, if we know that probability of any outcome outside those bounds is zero. For the temperature example, we could have a lower bound of {$-273.15\,^{\circ}{\rm C}$}, since the probability that the temperature in Wu & Chen is less than absolute zero should be zero.
In general, we'll be pretty loose with notation, so we might say a random variable takes on the value "heads" or "tails" when formally it should be mapped to a unique number. You don't need to worry too much about it for this class.
Probability Distributions
For any discrete random variable, we can define a corresponding discrete distribution. A discrete distribution maps the values of a discrete random variable to their probabilities of occurring. So, for the stone example above, the distribution would map 1 to 0.05, 2 to 0.05, 3 to 0.4, 4 to 0.05, 5 to 0.05, and 6 to 0.4. Again, note that the sum of the probability over all possible outcomes is 1.
Similarly, for continuous random variables, continuous distributions exist. The main point to keep in mind about continuous distributions is that because their set of outcomes is uncountable, they assign probability zero to any single value of a random variable. Returning to our temperature example, suppose we had a probability distribution for Wu & Chen temperatures between {$15\,^{\circ}{\rm C}$} and {$30\,^{\circ}{\rm C}$}. Then {$p(20)$}, probability of the single temperature value {$20\,^{\circ}{\rm C}$} would 0, as would {$p(20.1)$}, {$p(20.2)$}, etc. However, probability of a range of temperatures, say all temperatures from 20 to 20.2, could be non-zero.
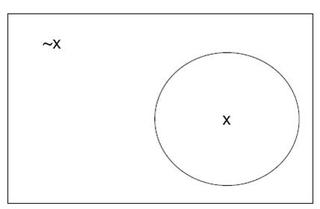
Distributions are sometimes visualized with Venn diagrams. In the picture below, we have a binary random variable {$X$}, which can take on one of two values: a default value that is written as {$X$}, and the opposite value, {$\sim\!\! X$}. The area inside the circle represents the probability that {$X$} equals the default value, and the area outside the circle represents the remainder of the probability mass.
Diagrams can get more interesting as we add more random variables ...
Joint Distributions
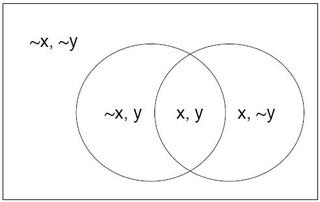
A joint distribution looks at the probability of more than one random variable. If there are only two random variables, this is called bivariate. An example of a bivariate distribution would be if we had one random variable representing a first coin flip and another random variable representing a second coin flip. If {$X$} represents the event that the first flip is a heads, and {$Y$} represents the event that the second flip is a heads, then we can draw a Venn diagram with one circle for each of these events, and their overlapping region would represent both flips being heads:
If there are more than two random variables in a distribution, then it is called multivariate.
Marginalization
In a given collection of random variables, we are often interested in only a subset of them. For example, we might want to compute {$p(X)$} from a joint distribution {$p(X, Y, Z)$}. Summing over all possible combinations of values for {$Y$} and {$Z$} to compute {$p(X)$} is called marginalizing out {$Y$} and {$Z$}. For example, suppose {$Y$} can take on the values 1 and 2 (e.g. to represent heads and tails), and {$Z$} can also take on the values 1 and 2. Then {$p(X)$} can be computed from the joint distribution as follows:
{$ \; \begin{align*} p(X) & = \sum_{Y} \sum_{Z} p(X, Y, Z) \\ & = \; p(X, Y = 1, Z = 1) + p(X, Y = 1, Z = 2) + p(X, Y = 2, Z = 1) + p(X, Y = 2, Z = 2) \end{align*} \; $}
PDFs and CDFs
We've looked at some Venn diagrams for probability distributions, but a more common and quantitative way to illustrate a probability distribution is by a probability density function (PDF). A PDF maps each value a random variable can take on to its probability. It's also common to see cumulative distribution functions (CDFs). A CDF illustrates for each possible value {$x$} of a random variable {$X$} the sum of probabilities for all values less than or equal to {$x$}: {$p(X \leq x)$}. A PDF and CDF are shown below for the stone tossing example.
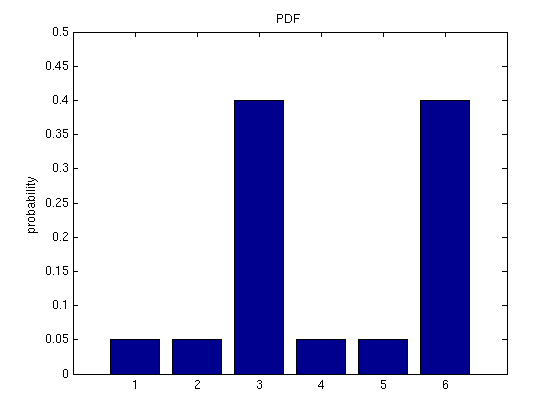
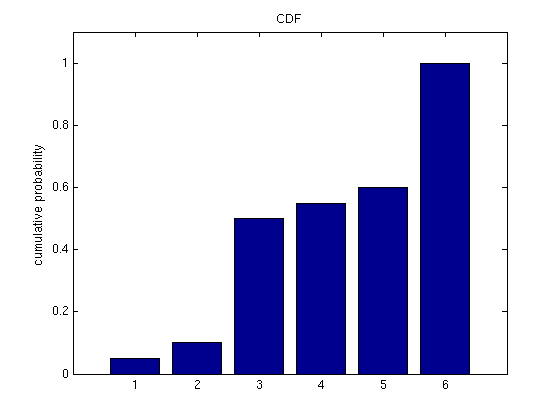
Expectation and Variance
Now that we have established some basics about what distributions are, let's look at a couple of measures that are often used to "summarize" them. First of all, there is the expected value of a distribution, also called the mean. It is exactly what you would expect --- the average value of the distribution. For a discrete variable {$X$}, this is defined as:
{$E_x[X] = \sum_x p(x)x$}
where the subscript {$X$} indicates that this is expectation is "with respect to {$p(x)$}". We'll often drop the subscript if it's clear from the context what distribution the expectation is with respect to. Here, if instead the expectation was with respect to say {$p(x,y)$} we would write this as:
{$E_{x,y}[X] = \sum_{x,y} p(x,y)x.$}
We can also take the expectation of a function {$f$} with respect to a probability distribution. Instead of the result being the average value of the distribution, it will be the average value of the function, where each function point is weighted by its probability under the distribution:
{$E_x[f(X)] = \sum_x p(x)f(x).$}
A second important summarizing measure for a distribution is variance. The variance tells us how spread out a distribution is. If a distribution is very concentrated around its mean, variance will be small. The formula for variance is:
{$Var_x[X] = \sum_x p(x)(x - \mu)^2$}
where {$\mu$} represents {$E_x[X]$}; this is a common notation we will often use for brevity. We'll also often denote {$Var_x[X]$} as simply {$\sigma^2$}.
Conditional Probability
So far the event combinations we considered are essentially just unions or intersections. What if instead we already know that a particular event occurred, and given that information want to know what the probability of a second event is? For example, if someone tells me that the last stone's throw resulted in a prime number, what is the probability that it was odd? First, let's call the event that the stone is prime {$A$} and the event that it is odd {$B$}. We want to know "probability of {$B$} given {$A$}". What does knowing {$A$} do for us? It reduces our outcome space to just 3 values: {$\{2, 3, 5\}$}. Since the total probability of an outcome space must sum to 1, we simply re-normalize:
{$p(2\; \textrm{given}\; A) = p(2 \mid A) = \frac{p(2)}{p(A)} = \frac{p(2)}{p(2) + p(3) + p(5)} = \frac{0.05}{0.05 + 0.05 + 0.4} = 0.1$}
Similarly, we can find {$p(3 \mid A) = 0.8$} and {$p(5 \mid A) = 0.1$}. Then, applying event union to combine the outcomes 3 and 5, we arrive at the solution that overall probability of odd given prime is 0.8 + 0.1 = 0.9.
Put in a slightly more abstract form, if we have two events {$A$} and {$B$}, (and we know that event {$A$} has a non-zero probability), then the probability of {$B$} occurring if {$A$} is already known is:
{$p(B \mid A) = \frac{p(A \cap B)}{p(A)}$}
Note that it is common to see {$p(A \cap B)$} as {$p(A, B)$} or {$p(AB)$}. (This does not mean {$p(A) \times p(B)$}!)
Bayes Rule
So, now we can calculate {$p(B \mid A)$}. What if we want to know the opposite probability, {$p(A \mid B)$}? If we knew {$p(B)$} and {$p(A \cap B)$}, we could just apply the definition of conditional probability from above and write it as:
{$p(A \mid B) = \frac{p(A \cap B)}{p(B)}.$}
If we don't know {$p(A \cap B)$} explicitly, but we have {$p(B \mid A)$}, we can also write this as:
{$p(A \mid B) = \frac{p(B \mid A)p(A)}{p(B)}.$}
To see why this is true, note that applying the definition of conditional probability twice gives us two definitions of {$p(A \cap B)$}:
{$p(A \mid B) = \frac{p(A \cap B)}{p(B)} \longrightarrow p(A \cap B) = p(A \mid B) p(B)$}
{$p(B \mid A) = \frac{p(A \cap B)}{p(A)} \longrightarrow p(A \cap B) = p(B \mid A) p(A)$}
and setting these two equations equal we get:
{$p(A \cap B) = p(A \mid B) p(B) = p(B \mid A) p(A)$}
which, with a little algebra is:
{$p(B|A) = \frac{p(A \mid B) p(B)}{p(A)}.$}
This is known as Bayes rule. We'll use Bayes rule a lot in class, so be sure to check out the examples of its use at the end of this page.
The Chain Rule
If we have a joint distribution of several variables, then we can apply the definition of conditional probability to rewrite the joint distribution as a product of conditional distributions:
{$p(X,Y) = \frac{p(X, Y)}{p(Y)} p(Y) = p(X \mid Y) p(Y)$}.
We can in fact apply this not just to the case of a bivariate distribution, but also to an {$N$}-variable multivariate distribution:
{$p(X_{1}, \ldots , X_{N}) = \prod_{n = 1}^N p(X_{n} \mid X_{1}, \ldots, X_{n-1})$}
This general formula is called the chain rule, and we will also be using it fairly often in this class.
Independence
In the introductory example with the stone, we mentioned the term i.i.d, independent and identically distributed. There, the term "independent" referred to the fact that two different samples from two different stone tosses did not affect each other. If you think of two tosses as two random variables {$X$} and {$Y$}, we denote that they are independent by {$X \perp Y$}. Formally, two random variables are independent if and only if {$p(X \cap Y) = p(X)p(Y)$}. From this definition, it's easy to see that we also get the following properties:
- {$p(X \mid Y) = \frac{p(X \cap Y)}{p(Y)} = \frac{p(X)p(Y)}{p(Y)} = p(X)$}
- {$p(Y \mid X) = p(Y)$}
Let's see if these match our intuition on a coin-flipping example. Let {$X$} represent a first coin flip and {$Y$} represent a second flip. These flips are independent. Thus, one statement we can make based on the above equations is that {$p(Y =\; \textrm{heads} \mid X =\; \textrm{heads}) = p(Y =\; \textrm{heads})$}. This makes sense, since the chance that the first toss was heads is not affected by knowing that the second toss was heads.
Conditional Independence
Some random variables that are not independent are still conditionally independent. Suppose {$X$} and {$Y$} are not independent, so knowing {$Y$} changes our belief about the probabilities of the values {$X$} can take on. Now, there may exist a third variable {$Z$} such that once {$Z$} is known, knowledge of {$Y$} does not change our belief about {$X$}. This conditional independence is denoted {$X \perp Y \mid Z$}, and it implies the following properties:
- {$p(X \mid Z, Y) = p(X \mid Z)$}
- {$p(Y \mid Z, X) = p(Y \mid Z)$}
- {$p(X, Y \mid Z) = p(X \mid Z) p(Y \mid Z)$}
Here's an intuitive example of conditional independence: Suppose you have a flight to catch, and {$M$} represents missing your plane, {$T$} represents that you encounter a swarm of tarantulas on the road to the airport, and {$S$} represents that you are gifted with the superpower of being able to drive through tarantula swarms without even slowing down. Now, without knowing {$S$}, knowing {$T$} might make me more inclined to believe you missed your plane. Similarly, without knowing {$S$}, knowing you missed your plane might make me more inclined to believe you encountered a swarm of tarantulas. However, if I know you have the superpower {$S$}, then knowing {$T$} doesn't have any effect on my belief about whether you made your plane or not.
Example Problems
The two child problem asks the following question: I have two children, and at least one of them is a son. What is the probability that both children are boys?
At first glance, it appears that the probability is {$\frac{1}{2}$}. The gender of one child has no effect on the gender of the other. However, knowing the gender of one child still has an effect on the probability that both are boys. Here is a table of the possible family makeups that should make this clear:
| First child | Second child |
|---|---|
| Boy | Boy |
| Boy | Girl |
| Girl | Boy |
The probability that both children are boys is actually {$\frac{1}{3}$}. Now, rather than listing all combinations to get the solution, we can come to the same conclusion simply using Bayes rule. Let {$p(B)$} be the probability that at least one child is a boy. Since this occurs in {$\frac{3}{4}$} cases, {$p(B) = \frac{3}{4}$}. Let the probability that both children are boys be {$p(BB) = \frac{1}{4}$}. Finally, we know that {$p(B \mid BB) = 1$}; this makes sense because it says that if we know both children are boys, than the probability that at least one is a boy is 1. So, combining everything together:
{$p(BB \mid B) = \frac{p(B \mid BB) p(BB)}{p(B)} = \frac{1 \times\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3}.$}
The Tuesday Child Problem
Now for a more difficult problem in the same vein, the Tuesday child problem. The problem is this: I have two children, and at least one is a son born on a Tuesday. What is the probability that I have two boys?
At first glance, it appears that the "born on a Tuesday" fact is unimportant, but this is not so. First, let's see why by listing all allowable outcomes. Each outcome is a quadruple (gender of child 1, day of birth of child 1, gender of child 2, day of birth of child 2).
Case 1: First, let's assume the first child to be a boy born on a Tuesday. Then the second child could be a boy or a girl and could be born on any day of the week. This would give us 14 possibilities, with 7 "good" events (both children boys) out of 14 possible.
Case 2: Now let's consider the other set of possibilities, where the second child is a boy born on a Tuesday; one of the possibilities here, the one where the second child is a boy born on a Tuesday and the first child is a boy born on a Tuesday was already covered in our "Case 1" analysis. Thus, there are only 13 new outcomes from considering this case, with only 6 "good" events (both children boys) out of 13 possible.
Overall, we have that the probability of both children being boys is {$\frac{7 + 6}{14 + 13} = \frac{13}{27}$}.
Now let's repeat this computation, but using Bayes rule. First off, we'll define some notation for the interesting events:
| Event | Symbol |
|---|---|
| At least one child is a boy born on a Tuesday | B |
| Both children are boys | BB |
| Elder child is a boy, younger is a girl | BG |
| Elder child is a girl, younger is a boy | GB |
| Both children are girls | GG |
Our goal then is to compute:
{$p(BB \mid B) = \frac{p(B \mid BB) \times p(BB)}{p(B)}.$}
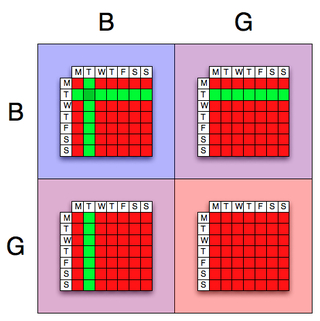
Now, to calculate {$p(B)$} we need to first calculate the conditional probability that at least one child is a son born on a Tuesday, given that the children are BB, BG, GB, or GG. The picture below should help make these computations clear:
{$ \begin{align*} p(B \mid BB) = & \frac{13}{49} \\ p(B \mid BG) = & \frac{1}{7} \\ p(B \mid GB) = & \frac{1}{7} \\ p(B \mid GG) = & 0. \end{align*} $}
To get {$p(B)$}, we can just sum {$p(B \mid BB) p(BB)$}, {$p(B \mid BG)p(BG)$}, {$p(B \mid GB)p(GB)$} and {$ p(B \mid GG)p(GG) $} :
{$p(B) = (\frac{13}{49} + \frac{1}{7} + \frac{1}{7}} + 0)\times\frac{1}{4} = \frac{27}{49}\times\frac{1}{4}$}
Finally, we can apply Bayes rule:
{$p(BB \mid B) = \frac{p(B \mid BB) \times p(BB)}{p(B)} = \frac{\frac{13}{49} \times \frac{1}{4}}{\frac{27}{49}\times\frac{1}{4}} = \frac{13}{27}$}
Note that {$\frac{13}{27}$} is quite different from {$\frac{1}{3}$}, the answer to the two child problem. In fact, {$\frac{13}{27}$} is very nearly {$\frac{1}{2}$}. What if we generalize the Tuesday child problem like so: I have two children, and one is a boy born no later than day {$N$} for {$N$} in {$1, \ldots, 7$}. What is the probability I have two boys? If you work out the math with Bayes rule, the results show a progression from {$\frac{1}{2}$} to {$\frac{1}{3}$}. The value {$\frac{1}{2}$} actually shows up at {$N = 0$}, because the constraint "one boy is born no later than day 0" is like having one of the children not exist, in which case we're just asking the probability that some child is a boy.
| N | Probability |
|---|---|
| 0 | 14/28 = 1/2 |
| 1 | 13/27 |
| 2 | 12/26 |
| 3 | 11/25 |
| 4 | 10/24 |
| 5 | 9/23 |
| 6 | 8/22 |
| 7 | 7/21 = 1/3 |
The Beach Problem
Suppose you are thinking of going to the beach. Let's have {$B$} denote that you go to the beach, and {$\neg B$} denote that you do not go. Also, let's have {$I$} represent the event of eating ice cream, and {$D$} represent the event of drowning. Assuming {$I$} and {$D$} are conditionally independent given {$B$} or {$\neg B$}, determine whether {$I$} and {$D$} are also independent, using the five probabilities below.
{$p(I \mid B) = 0.7,\; p(I \mid \neg B) = 0.4,\; p(D \mid B) = 0.6,\; p(D \mid \neg B) = 0.2,\; p(B)= 0.3 $}
Our goal is to determine whether {$p(I, D) = p(I)p(D)$} is true, given the above probabilities and the fact that {$p(I, D \mid B) = p(I \mid B)p(D \mid B)$} and {$p(I, D \mid \neg B) = p(I \mid \neg B)p(D \mid \neg B)$}:
{$ \; $ \begin{align*} p(I) & = \; p(I \mid B)p(B) + p(I \mid \neg B)p(\neg B) \\ & = \; (0.7 \times 0.3) + (0.4 \times 0.7) = 0.21 + 0.28 = 0.49 \\ p(D) & = \; p(D \mid B)p(B) + p(D \mid \neg B)p(\neg B) \\ & = \; (0.6 \times 0.3) + (0.2 \times 0.7) = 0.18 + 0.14 = 0.32 \\ p(I)p(D) & = \; 0.49 * 0.32 = 0.1568 \\ p(I, D) & = \; p(I,D \mid B)P(B) + p(I,D \mid \neg B)p(\neg B) \\ & = \; p(I \mid B)p(D \mid B)p(B) + p(I \mid \neg B)p(D \mid \neg B)p(\neg B) \\ & = \; (0.7 \times 0.6 \times 0.3) + (0.4 \times 0.2 \times 0.7) = 0.126 + 0.056 = 0.182 \end{align*} $ \; $}
Since {$ 0.1568 \ne 0.182 $}, eating ice cream and drowning are not independent. Thus, eating ice cream and drowning are correlated. As ice cream consumption increases, the number of people drowning also increases. But eating ice cream doesn't cause drowning and drowning doesn't make people buy ice cream. Rather, this is a case of "correlation doesn't imply causation" (see also xkcd). Being at the beach on a hot day causes people both to swim (which brings the risk of drowning) and to eat ice cream due to the heat. Being at the beach is the causal third variable that establishes the correlation between eating ice cream and drowning.
Monty Hall Problem
The Monty Hall Problem is yet another strange result of applying rules of probability. The Monty Hall Problem asks the following question:
Intuitively, most people would say that it doesn't matter if you switch or not. However, switching your choice will in fact double your chance of winning the car. Let's examine why this is the case. At the time of your initial door selection, the probability that you select the car {$C1$} is {$\frac{1}{3}$} and the probability you select a goat {$\neg C1$} is {$\frac{2}{3}$}. Let's call the event that you end up with the car after your second door selection (either switching or not switching) {$C2$}. We'll compute {$p(C2)$} for both the switching and not-switching scenarios to show that switching is better.
If you switch then:
- Case {$C1$}: You selected the door with the car (probability {$\frac{1}{3}$}). Then the host opens one of the goat doors. Switching doors, you will get a goat ({$p(C2 \mid C1) = 0$}).
- Case {$\neg C1$}: You selected a door with a goat (probability {$\frac{2}{3}$}). Then the host opens the other goat door. Switching doors, you will get a car ({$p(C2 \mid \neg C1) = 1$}).
So, overall we have that:
{$p(C2) = p(C1)p(C2 \mid C1) + p(\neg C1)p(C2 \mid \neg C1) = (\frac{1}{3} \times 0) + (\frac{2}{3} \times 1) = \frac{2}{3}.$}
In the other scenario, where you don't switch, we instead have that:
{$p(C2) = (\frac{1}{3} \times 1) + (\frac{2}{3} \times 0) = 1/3$}.
Thus, switching is twice as likely to win you a car as not switching. Back to Lectures