On this page… (hide)
The Naive Bayes classifier is an example of the generative approach: we will model {$P(\mathbf{x},y)$}. Consider the toy transportation data below:
| x: Inputs/Features/Attributes | y: Class | ||
|---|---|---|---|
| Distance(miles) | Raining | Flat Tire | Mode |
| 1 mile | no | no | bike |
| 2 miles | yes | no | walk |
| 1 mile | no | yes | bus |
| 1 mile | yes | no | walk |
| 2 miles | yes | no | bus |
| 1 mile | no | no | car |
| 1 mile | yes | yes | bike |
| 10 miles | yes | no | bike |
| 10 miles | no | no | car |
| 4 miles | no | no | bike |
We will decompose {$P(\mathbf{x},y)$} into class prior and class model:
{$P(\mathbf{x},y) = \underbrace{P(y)}_{\rm class prior} \underbrace{P(\mathbf{x}\mid y)}_{\rm class model}$}
and estimate them separately as {$\hat{P}(y)$} and {$\hat{P}(\mathbf{x} \mid y)$}. (Class prior should not be confused with parameter prior. They are very similar concepts, but not the same things.)
We will then use our estimates to output a classifier using Bayes rule:
{$ \begin{align*} h(\mathbf{x}) & = \arg\max_y \;\;\hat{P}(y\mid \mathbf{x}) \\ & = \arg\max_y \;\;\;\; \frac{\hat{P}(y)\hat{P}(\mathbf{x} \mid y)}{\sum_{y'}\hat{P}(y')\hat{P}(\mathbf{x} \mid y')} \\ & = \arg\max_y \;\;\;\; \hat{P}(y)\hat{P}(\mathbf{x} \mid y) \end{align*} $}
To estimate our model using MLE, we can separately estimate the two parts of the model:
{$ \begin{align*} \log P(D) & = \sum_i \log P(\mathbf{x}_i,y_i) \\ & = \sum_i \log P(y_i) + \log P(\mathbf{x}_i \mid y_i) \\ & = \log P(D_Y) + \log P(D_X | D_Y) \end{align*} $}
How do we estimate {$P(y)$}? This is very much like the biased coin, except instead of two outcomes, we have 4 (walk, bike, bus, car). We need 4 parameters to represent this multinomial distribution (3 really, since they must sum to 1): {$(\theta_{\rm walk},\theta_{\rm bike},\theta_{\rm bus},\theta_{\rm car})$}. The MLE estimate (deriving it is a good exercise) is {$\hat{\theta}_y = \frac{1}{n}\sum_i \textbf{1}(y=y_i)$}.
| y | parameter {$\theta_{y}$} | MLE {$\hat{\theta}_{y}$} |
|---|---|---|
| walk | {$\theta_{\rm walk}$} | 0.2 |
| bike | {$\theta_{\rm bike}$} | 0.4 |
| bus | {$\theta_{\rm bus}$} | 0.2 |
| car | {$\theta_{\rm car}$} | 0.2 |
Estimating class models is much more difficult, since the joint distribution of m dimensions of {$\textbf{x}$} can be very complex. Suppose that all the features are binary, like Raining or Flat Tire above. If we have m features, there are {$K*2^m$} possible values of {$(\textbf{x},y)$} and we cannot store or estimate such a distribution explicitly, like we did for {$P(y)$}. The key (naive) assumption of the model is conditional independence of the features given the class. Recall that {$X_k$} is conditionally independent of {$X_j$} given Y if:
{$P(X_j=x_j \mid X_k=x_k, Y=y)= P(X_j=x_j \mid Y=y), \; \forall x_j,x_k,y$}
or equivalently,
{$ \begin{align*} P(X_j=x_j,X_k=x_k\mid Y=y) & = \\ & P(X_j=x_j\mid Y=y)P(X_k=x_k\mid Y=y),\forall x_j,x_k,y \end{align*} $}
More generally, the Naive Bayes assumption is that:
{$\hat{P}(\mathbf{X}\mid Y) = \prod_j \hat{P}(X_j\mid Y)$}
Hence the Naive Bayes classifier is simply:
{$\arg\max_y \hat{P}(Y=y \mid \mathbf{X}) = \arg\max_y \hat{P}(Y=y)\prod_j \hat{P}(X_j\mid Y=y)$}
If the feature {$X_j$} is discrete like Raining, then we need to estimate K distributions for it, one for each class, {$P(X_j | Y = k)$}. We have 4 parameters, ({$\theta_{{\rm R}\mid\rm walk}, \theta_{{\rm R}\mid\rm bike}, \theta_{{\rm R}\mid\rm bus}, \theta_{{\rm R}\mid\rm car}$}), denoting probability of Raining=yes given transportation taken. The MLE estimate (deriving it is also a good exercise) is {$\hat{\theta}_{{\rm R}\mid y} = \frac{\sum_i \textbf{1}(R=yes, y=y_i)}{\sum_i \textbf{1}(y=y_i)}$}. For example, {$P({\rm R}\mid Y)$} is
| y | parameter {$\theta_{{\rm R}\mid y}$} | MLE {$\hat{\theta}_{R \mid y}$} |
|---|---|---|
| walk | {$\theta_{{\rm R}\mid\rm walk}$} | 1 |
| bike | {$\theta_{{\rm R}\mid\rm bike}$} | 0.5 |
| bus | {$\theta_{{\rm R}\mid\rm bus}$} | 0.5 |
| car | {$\theta_{{\rm R}\mid\rm car}$} | 0 |
For a continuous variable like Distance, there are many possible choices of models, with Gaussian being the simplest. We need to estimate K distributions for each feature, one for each class, {$P(X_j | Y = k)$}. For example, {$P({\rm D}\mid Y)$} is
| y | parameters {$\mu_{{\rm D}\mid y}$} and {$\sigma_{{\rm D}\mid y}$} | MLE {$\hat{\mu}_{{\rm D}\mid y}$} | MLE {$\hat{\sigma}_{{\rm D}\mid y}$} |
|---|---|---|---|
| walk | {$\mu_{{\rm D}\mid\rm walk}$},{$\sigma_{{\rm D}\mid\rm walk}$} | 1.5 | 0.5 |
| bike | {$\mu_{{\rm D}\mid\rm bike}$}, {$\sigma_{{\rm D}\mid\rm bike}$} | 4 | 3.7 |
| bus | {$\mu_{{\rm D}\mid\rm bus}$}, {$\sigma_{{\rm D}\mid\rm bus}$} | 1.5 | 0.5 |
| car | {$\mu_{{\rm D}\mid\rm car}$}, {$\sigma_{{\rm D}\mid\rm car}$} | 5.5 | 4.5 |
Note that for words, instead of using a binary variable (word present or absent), we could also use the number of occurrences of the word in the document, for example by assuming a binomial distribution for each word.
Note the danger of using MLE estimates. For example, consider the estimate of conditional distribution of Raining=yes: {$\hat{P}({\rm Raining = yes} \mid y={\rm car}) = 0$}. So if we know it’s raining, no matter the distance, the probability of taking the car is 0, which is not a good estimate. This is a general problem due to scarcity of data: we never saw an example with car and raining. Using MAP estimation with Beta priors (with {$\alpha,\beta>1$}), estimates will never be zero, since additional “counts” are added.
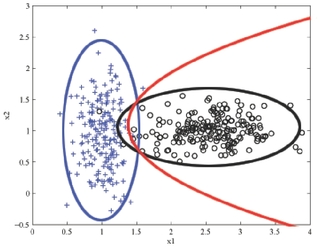
Suppose our data is from two classes (plus and circle) in two dimensions ({$x_1$} and {$x_2$}) and looks like this:
The Naive Bayes classifier will estimate a Gaussian for each class and each dimension. We can visualize the estimated distribution by drawing a contour of the density. The decision boundary, where the probability of each class given the input is equal, is shown in red.
In classifying text documents, like news articles or emails or web pages, the input is a very complex, structured object. Fortunately, for simple tasks like deciding about spam vs. not spam, politics vs sports, etc., a very simple representation of the input suffices. The standard way to represent a document is to completely disregard the order of the words in it and just consider their counts. So the email below might be represented as:
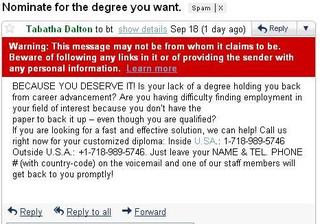
The Naive Bayes classifier then learns {$\hat{P}(spam)$}, and {$\hat{P}(word\mid spam)$} and {$\hat{P}(word \mid ham)$} for each word in our dictionary by using MLE/MAP as above. It then predicts prediction ‘spam’ if:
{$\hat{P}(spam)\prod_{{\rm word} \in {\rm email}} \hat{P}(word\mid spam) > \hat{P}(ham)\prod_{{\rm word} \in {\rm email}} \hat{P}(word\mid ham)$}