|
Home
|
SOLUTIONS OF THE SELF TEST PROBLEMS
- Bayes Rule: P(X|E)= P(E|X)P(X)/P(E)
The weatherman has predicted rain tomorrow. In recent years, it has rained only 73 days each year. When it actually rains, the weatherman correctly forecasts rain 70% of the time. When it doesn’t rain, he incorrectly forecasts rain 30% of the time. What is the probability that it will rain tomorrow?
The sample space is defined by two mutually-exclusive events - it rains or it does not rain. Additionally, a third event occurs when the weatherman predicts rain. Notation for these events appears below.
- Event {$A_{1}$}: It rains tomorrow.
- Event {$A_{2}$}: It does not rain tomorrow.
- Event B: The weatherman predicts rain.
We know the following in terms of probabilities:
- P( A1 ) = 73/365 =0.2 [It rains 73 days out of the year.]
- P( A2 ) = 292/365 = 0.8 [It does not rain 292 days out of the year.]
- P( B | A1 ) = 0.7 [When it rains, the weatherman predicts rain 70% of the time.]
- P( B | A2 ) = 0.3 [When it does not rain, the weatherman predicts rain 30% of the time.]
We want to know P( A1 | B ), the probability it will tomorrow, given a forecast for rain by the weatherman. The answer can be determined from Bayes’ theorem, as shown below.
- P( A1 | B ) = P( A1 ) P( B | A1 ) / [ P( A1 ) P( B | A1 ) + P( A2 ) P( B | A2 ) ]
- P( A1 | B ) = (0.2)(0.7) / [ (0.2)(0.7) + (0.8)(0.3) ]
- P( A1 | B ) = 0.37
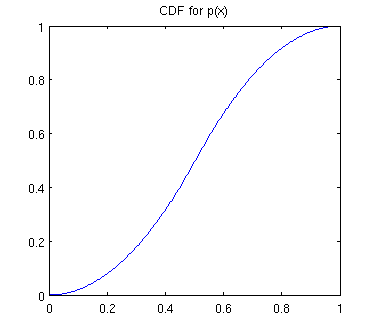
- We are given that the pdf is
{$ p(x) = \left\{ \begin{array}{ll} 4x & 0 \le x \le 1/2 \\ -4x+4 & 1/2 \le x \le 1\end{array} \right. $}
What is the equation and graph its cdf P(x)?
P(x) is an anti-derivative of p(x), so integrating the terms of p(x) we get:
{$ p(x) = \left\{ \begin{array}{ll} 2x^2 + A & 0 \le x \le 1/2 \\ -2x^2 + 4x + C & 1/2 \le x \le 1\end{array} \right. $}
A and C are the constants of integration. P(x) must go to 0 as moved to the left and it is assumed that P(x) starts at 0. Therefore P(0) = 0 = 2(0)2 + A; and so A = 0. P(x) must go to 1 as moved to the right and it is assumed that P(x) ends at 1. Therefore P(1) = 1 = −2(1)2 + 4(1) + C; and so C = −1. As a result P(x) can be written as:
{$ p(x) = \left\{ \begin{array}{ll} 2x^2 & 0 \le x \le 1/2 \\ -2x^2 + 4x - 1 & 1/2 \le x \le 1\end{array} \right. $}
- Calculate the expected value of {$X$}, {$E[X]$}, where {$X$} is a random variable representing the outcome of a roll of a trick die. Use the sample space {$x \in \{1,2,3,4,5,6\}$} and let
{$p(X=x) = \left\{ \begin{array}{ll} 1/2 & x=1 \\ 1/10 & x\neq 1 \end{array} \right $}.
Recall that the definition of the expected value of a discrete random variable is:
{$E[X]=\sum_{i} p(x_i)x_i $}
Therefore, in this case, we have {$E[X] = 1/2 + 2/10 + 3/10 + 4/10 + 5/10 + 6/10 = 25/10 = 2.5$}. Note that 2.5 is not a possible outcome, and be aware that expectations may not be in the sample space.
- Use the properties of expectation to show that we can rewrite the variance of a random variable X as
{$ Var[X] = E[X^2] - (E[X])^2 $}
If a random variable X has the expected value (mean) {$\mu = E[X]$}, then the variance of X is given by:
{$ Var[X] =E[(X - \mu)^2] $}
{$ Var[X] = E[X^2 - 2\mu X + \mu^2] $}
{$ Var[X] = E[X^2] - 2\mu E[X] + \mu^2 $}
{$ Var[X] = E[X^2] - 2\mu^2 + \mu^2 $}
{$ Var[X] = E[X^2] - \mu^2 $}
{$ Var[X] = E[X^2] - (E[X])^2 $}
- Consider the following system of equations:
{$ \begin{array}{ccccccc} 2 x_{1} & + & x_{2} & + & x_{3} & = & 3, \\ 4x_{1} & & & + & 2x_{3} & = & 10, \\ 2 x_{1} & + & 2x_{2} & & & = & -2. \end{array} $}
- Write the system as a matrix equation of the form {$Ax = b . $}
{$ A= \left(\begin{array} {ccc} 2 & 1 & 1 \\ 4 & 0 & 2\\ 2 & 2 & 0 \end{array}\right)$} and {$ x= \left(\begin{array} {ccc} x_{1} \\ x_{2}\\ x_{3} \end{array}\right)$} and {$ b= \left(\begin{array} {ccc} 3 \\ 10\\ -2 \end{array}\right)$}
- Write the solution of the system as a column {$S$} and verify by matrix multiplication that {$S $} satisfies the equation {$Ax = b . $}
{$ s= \left(\begin{array} {ccc} 1 \\ -2\\ 3 \end{array}\right)$}
- Write {$b $} as a linear combination of the columns in {$A. $}
{$ b = A_{*1} - 2A_{*2} + 3A_{*3} $}
- Consider the following matrix:
{$\left[\begin{array}{ccc} 1 & 2 & 3 \\ 1 & 4 & 3\\ 1 & 3 & 4 \end{array}\right]$}
- Is the matrix invertible? (Hint: think about singularity and determinants…)
The answer is yes; remember that a matrix is invertible if it is non-singular (i.e. the determinant is not equal to zero). Remember for a 3×3 matrix A:
{$A = \left\[\begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array}\right\]$}
that the determinant is defined as:
{$det(A) = aei + bfg + cdh - afh - ceg - bdi $}
So we have that the determinant of the above matrix is: {$16 + 6 + 9 - 9 - 8 -12 = 2$}
- What’s the rank of the matrix?
The rank of a matrix is the number of linearly independent columns (or rows, they’re interchangeable). For this answer, it’s easy, since a matrix cannot be invertible unless it has full rank, meaning all columns(rows) are linearly independent; so {$rk(A) = 3$}. One can calculate rank by performing Gaussian elimination and counting the non-zero rows. See Wikipedia for more information.
- The eigenvalues of the matrix:
{$ A= \left[\begin{array} {cc} 3 & 6 \\ 1 & 4 \end{array}\right]$} {$\quad$} are {$\lambda = 6$} and {$ \lambda\ = 1.$}
Which of the following is an eigenvector for {$\lambda= 1? $}
Just remember that a vector is an eigenvector for a transformation (i.e. matrix) and an eigenvalue if the following is true:
{$Ax = \lambda x$}
Given that we must find the eigenvector for the eigenvalue of 1, we get:
{$Ax = x$}
We can check each given eigenvector by plugging it into the following system:
{$\begin{array}{ccc}3x + 6y & = & x\\x + 4y & = & y \end{array} $}
This yields {$\left[\begin{array} {c} -3\\ 1\end{array}\right]$} as an eigenvector for {$\lambda = 1.$}
- Find the 0, 1, 2 and {$\infty$} norms of
{$ x= \left(\begin{array} {c}2 \\ 1\\-4 \\ -2 \end{array}\right)$} {$\quad$}
{$ \lim_{p \rightarrow 0} ||x||_{p}^{p} $} (The zero norm is the number of non-zero elements.)
{$ ||x||_{1} = \sum_{i=1}^{n} |x_{i}|$} (The grid norm)
{$ ||x||_{2} = \left(\sum_{i=1}^{n} |x_{i}|^{2}\right)^{1/2} $} (The euclidean norm)
{$ ||x||_{\infty} = \lim_{p \rightarrow \infty} ||x||_{p} = \lim_{p \rightarrow \infty} \left(\sum_{i=1}^{n} |x_{i}|^{p}\right)^{1/p} = \max_{i}|x_{i}|$} (The max norm)
The zero norm is 4 since it is the number of non-zero elements.
{$ ||x||_{1} = 9$}
{$ ||x||_{2} = 5$}
{$ ||x||_{\infty} = 4$}
Back to Lectures
|
