
|
Lectures /
Naive BayesOn this page… (hide) Naive Bayes ModelThe Naive Bayes classifier is an example of the generative approach: we will model {$P(\mathbf{x},y)$}. Consider the toy transportation data below:
We will decompose {$P(\mathbf{x},y)$} into class prior and class model: {$P(\mathbf{x},y) = \underbrace{P(y)}_{\rm class prior} \underbrace{P(\mathbf{x}\mid y)}_{\rm class model}$} and estimate them separately as {$\hat{P}(y)$} and {$\hat{P}(\mathbf{x} \mid y)$}. (Class prior should not be confused with parameter prior. They are very similar concepts, but not the same things.) We will then use our estimates to output a classifier using Bayes rule: {$ \begin{align*} h(\mathbf{x}) & = \arg\max_y \;\;\hat{P}(y\mid \mathbf{x}) \\ & = \arg\max_y \;\;\;\; \frac{\hat{P}(y)\hat{P}(\mathbf{x} \mid y)}{\sum_{y'}\hat{P}(y')\hat{P}(\mathbf{x} \mid y')} \\ & = \arg\max_y \;\;\;\; \hat{P}(y)\hat{P}(\mathbf{x} \mid y) \end{align*} $} To estimate our model using MLE, we can separately estimate the two parts of the model: {$ \begin{align*} \log P(D) & = \sum_i \log P(\mathbf{x}_i,y_i) \\ & = \sum_i \log P(y_i) + \log P(\mathbf{x}_i \mid y_i) \\ & = \log P(D_Y) + \log P(D_X | D_Y) \end{align*} $} Estimating {$P(y)$}How do we estimate {$P(y)$}? This is very much like the biased coin, except instead of two outcomes, we have 4 (walk, bike, bus, car). We need 4 parameters to represent this multinomial distribution (3 really, since they must sum to 1): {$(\theta_{\rm walk},\theta_{\rm bike},\theta_{\rm bus},\theta_{\rm car})$}. The MLE estimate (deriving it is a good exercise) is {$\hat{\theta}_y = \frac{1}{n}\sum_i \textbf{1}(y=y_i)$}.
Estimating {$P(\textbf{x}\mid y)$}Estimating class models is much more difficult, since the joint distribution of m dimensions of {$\textbf{x}$} can be very complex. Suppose that all the features are binary, like Raining or Flat Tire above. If we have m features, there are {$K*2^m$} possible values of {$(\textbf{x},y)$} and we cannot store or estimate such a distribution explicitly, like we did for {$P(y)$}. The key (naive) assumption of the model is conditional independence of the features given the class. Recall that {$X_k$} is conditionally independent of {$X_j$} given Y if: {$P(X_j=x_j \mid X_k=x_k, Y=y)= P(X_j=x_j \mid Y=y), \; \forall x_j,x_k,y$} or equivalently, {$ \begin{align*} P(X_j=x_j,X_k=x_k\mid Y=y) & = \\ & P(X_j=x_j\mid Y=y)P(X_k=x_k\mid Y=y),\forall x_j,x_k,y \end{align*} $} More generally, the Naive Bayes assumption is that: {$\hat{P}(\mathbf{X}\mid Y) = \prod_j \hat{P}(X_j\mid Y)$} Hence the Naive Bayes classifier is simply: {$\arg\max_y \hat{P}(Y=y \mid \mathbf{X}) = \arg\max_y \hat{P}(Y=y)\prod_j \hat{P}(X_j\mid Y=y)$} If the feature {$X_j$} is discrete like Raining, then we need to estimate K distributions for it, one for each class, {$P(X_j | Y = k)$}. We have 4 parameters, ({$\theta_{{\rm R}\mid\rm walk}, \theta_{{\rm R}\mid\rm bike}, \theta_{{\rm R}\mid\rm bus}, \theta_{{\rm R}\mid\rm car}$}), denoting probability of Raining=yes given transportation taken. The MLE estimate (deriving it is also a good exercise) is {$\hat{\theta}_{{\rm R}\mid y} = \frac{\sum_i \textbf{1}(R=yes, y=y_i)}{\sum_i \textbf{1}(y=y_i)}$}. For example, {$P({\rm R}\mid Y)$} is
For a continuous variable like Distance, there are many possible choices of models, with Gaussian being the simplest. We need to estimate K distributions for each feature, one for each class, {$P(X_j | Y = k)$}. For example, {$P({\rm D}\mid Y)$} is
MLE vs. MAPNote the danger of using MLE estimates. For example, consider the estimate of conditional distribution of Raining=yes: {$\hat{P}({\rm Raining = yes} \mid y={\rm car}) = 0$}. So if we know it’s raining, no matter the distance, the probability of taking the car is 0, which is not a good estimate. This is a general problem due to scarcity of data: we never saw an example with car and raining. Using MAP estimation with Beta priors (with {$\alpha,\beta>1$}), estimates will never be zero, since additional “counts” are added. Examples2-dimensional, 2-class exampleSuppose our data is from two classes (plus and circle) in two dimensions ({$x_1$} and {$x_2$}) and looks like this: The Naive Bayes classifier will estimate a Gaussian for each class and each dimension. We can visualize the estimated distribution by drawing a contour of the density. The decision boundary, where the probability of each class given the input is equal, is shown in red. 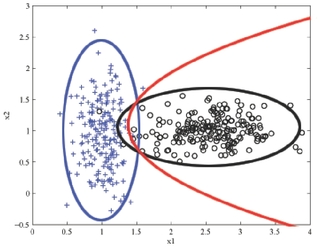 2D binary classification with Naive Bayes. A density contour is drawn for the Gaussian model of each class and the decision boundary is shown in red Text classification: bag-of-words representationIn classifying text documents, like news articles or emails or web pages, the input is a very complex, structured object. Fortunately, for simple tasks like deciding about spam vs. not spam, politics vs sports, etc., a very simple representation of the input suffices. The standard way to represent a document is to completely disregard the order of the words in it and just consider their counts. So the email below might be represented as: 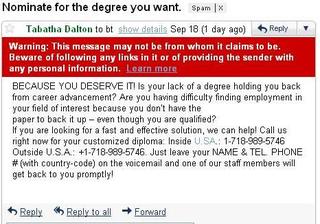 bag-of-words model for text classification: degree=1, diploma=1, customized=1, deserve=1, fast=1, promptly=1… The Naive Bayes classifier then learns {$\hat{P}(spam)$}, and {$\hat{P}(word\mid spam)$} and {$\hat{P}(word \mid ham)$} for each word in our dictionary by using MLE/MAP as above. It then predicts prediction ‘spam’ if: {$\hat{P}(spam)\prod_{{\rm word} \in {\rm email}} \hat{P}(word\mid spam) > \hat{P}(ham)\prod_{{\rm word} \in {\rm email}} \hat{P}(word\mid ham)$} |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||